广西壮族自治区防城港市防城区2024年八年级上学期期末数学试题
试卷更新日期:2024-01-24 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.)
-
1. 点关于轴的对称点的坐标是( )A、 B、 C、 D、2. 分式有意义的条件是( )A、 B、 C、 D、3. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若一个三角形的两边长分别为4和9,则第三边长可能是( )A、3 B、4 C、5 D、115. 下列运算正确的是( )A、 B、 C、 D、6. 在中,若 , , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 如图下列各组条件中,可以判定的条件是( )
4. 若一个三角形的两边长分别为4和9,则第三边长可能是( )A、3 B、4 C、5 D、115. 下列运算正确的是( )A、 B、 C、 D、6. 在中,若 , , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 如图下列各组条件中,可以判定的条件是( )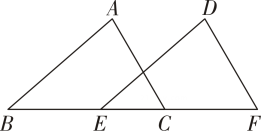 A、、、 B、、、 C、、、 D、、、、8. 正多边形的每一个外角都是 , 则这个正多边形的内角和是( )A、 B、 C、 D、9. 下列是最简分式的是( )A、 B、 C、 D、10. 如图,将一副三角板的直角顶点重合并部分重叠,若 , 则的度数为( )
A、、、 B、、、 C、、、 D、、、、8. 正多边形的每一个外角都是 , 则这个正多边形的内角和是( )A、 B、 C、 D、9. 下列是最简分式的是( )A、 B、 C、 D、10. 如图,将一副三角板的直角顶点重合并部分重叠,若 , 则的度数为( ) A、 B、 C、 D、11. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )
A、 B、 C、 D、11. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )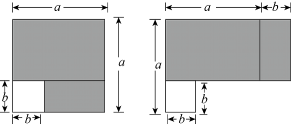 A、 B、 C、 D、12. 如图,在中, , , 的面积为12,于点 , 直线垂直平分交于点 , 交于点 , 是线段上的一个动点,分别连接 , , 则的周长的最小值是( )
A、 B、 C、 D、12. 如图,在中, , , 的面积为12,于点 , 直线垂直平分交于点 , 交于点 , 是线段上的一个动点,分别连接 , , 则的周长的最小值是( )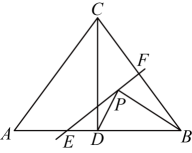 A、6 B、7 C、10 D、12
A、6 B、7 C、10 D、12二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 分解因式:.14. 白细胞是我们体内的重要免疫细胞,负责保护我们免受病原体的侵害.据研究,白细胞直径约为0.000012米,0.000012用科学记数法表示为.15. 2023年10月1日,杭州亚运会射击项目进入最后一个比赛日,中国射击队最终以16枚金牌的成绩结束本届亚运会,以较大优势占据射击项目金牌榜头名.射击队员在瞄准目标时,手、肘、肩构成托枪三角形,这种方法应用的几何原理是.
 16. 如图,边长为的正三角形向右平移 , 得到正三角形 , 此时阴影部分的周长为.
16. 如图,边长为的正三角形向右平移 , 得到正三角形 , 此时阴影部分的周长为. 17. 若 是完全平方式,则 的值等于 .18. 如图,在中, , 交于点 , , 则.
17. 若 是完全平方式,则 的值等于 .18. 如图,在中, , 交于点 , , 则.
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算:20. 解方程: .21. 在等腰三角形中,.
 (1)、画出的平分线,且与相交于点(尺规作图,保留作图痕迹);(2)、若 , 求的度数.22. 先化简,再求值: , 其中23. 如图,是的角平分线, , 交于点.
(1)、画出的平分线,且与相交于点(尺规作图,保留作图痕迹);(2)、若 , 求的度数.22. 先化简,再求值: , 其中23. 如图,是的角平分线, , 交于点. (1)、求证:.(2)、当时,请判断与的大小关系,并说明理由.24. 如图,点 , , , 在同一条直线上,点 , 分别在直线的两侧,且 , , .
(1)、求证:.(2)、当时,请判断与的大小关系,并说明理由.24. 如图,点 , , , 在同一条直线上,点 , 分别在直线的两侧,且 , , . (1)、求证:;(2)、若 , , 求的长.25. 【综合与实践】
(1)、求证:;(2)、若 , , 求的长.25. 【综合与实践】学校在某商场购买甲、乙两种不同类型的足球,相关信息如下:购买甲种足球共用2000元,购买乙种足球共花费1400元.已知购买一个乙种足球比购买一个甲种足球多花20元.设购买一个甲种足球的单价是元。
(1)、请用含的代数式分别表示购买甲、乙两种足球的数量;(2)、若本次购买甲种足球的数量是购买乙种足球数量的2倍,求甲、乙两种足球在此商场的销售单价;(3)、为满足学生需求,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的销售单价进行调整,甲种足球的销售单价比上次购买时提高了10%,乙种足球的销售单价比上次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2950元,求这所学校最多可以购买乙种足球的数量.26. 综合实践课上,老师让同学们以“三角形纸片的折叠”为主题开展数学活动 (1)、【操作发现】对折(),使点落在边上的点处,得到折痕 , 把纸片展平,如图1.小明根据以上操作发现:四边形满足 , .查阅相关资料得知,像这样的有两组邻边分别相等的四边形叫作“筝形”.请写出图1中筝形的一条性质.(2)、【探究证明】已知:如图2,在筝形中, , , 对角线、交于点.求证:(3)、【迁移应用】如图3,在中, , , 点、分别是边 , 上的动点,当四边形为筝形时,的度数为多少?
(1)、【操作发现】对折(),使点落在边上的点处,得到折痕 , 把纸片展平,如图1.小明根据以上操作发现:四边形满足 , .查阅相关资料得知,像这样的有两组邻边分别相等的四边形叫作“筝形”.请写出图1中筝形的一条性质.(2)、【探究证明】已知:如图2,在筝形中, , , 对角线、交于点.求证:(3)、【迁移应用】如图3,在中, , , 点、分别是边 , 上的动点,当四边形为筝形时,的度数为多少?