广西壮族自治区防城港市防城区2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-01-24 类型：期末考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分）

1. 2023的相反数是（）

A、-2023 B、 $| 2023 |$ C、 $- \frac{1}{2023}$ D、 $\frac{1}{2023}$

查看试题解析
2. 下列方程中，是一元一次方程的是（）

A、 $x^{2} + 3 = 0$ B、 $x + 3 = y + 2$ C、 $\frac{1}{x} = 4$ D、 $x = 0$

查看试题解析
3. 太阳中心的温度可达 $15500000 ℃$ ，用科学记数法表示正确的是（）

A、 $1.55 \times 1 0^{7}$ B、 $15.5 \times 1 0^{6}$ C、 $1.55 \times 1 0^{8}$ D、 $0.155 \times 1 0^{8}$

查看试题解析
4. 若+300表示收入300元，那 $- 150$ 元表示（）

A、支出 $- 150$ 元 B、支出150元 C、盈利150元 D、支出与收入相差150元

查看试题解析
5. 下列说法正确的是（）

A、2.9万精确到十分位 B、 $2.9 \times 1 0^{4}$ 精确十分位 C、2.9精确十分位 D、12950精确到万位

查看试题解析
6. 下列计算正确的是（）

A、 $a x + y = a x y$ B、 $- 5 a b + 5 b a = 0$ C、 $3 a^{2} + a = 4 a^{3}$ D、 $5 m^{3} - 2 m^{2} = 3 m$

查看试题解析
7. 下列四个图形中，经过折叠可以围成一个棱柱的是（）

A、 B、 C、 D、

查看试题解析
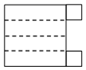8. 如图，线段 $C D = 2 c m$ ，点C是AB的中点，点D是AC的中点，则线段BD的长是（）．

A、5 B、6 C、8 D、10

查看试题解析
9. 若关于x的方程 $2 x = 8$ 与 $x + 2 = - k$ 的解相同，则k的值是（）

A、6 B、 $- 4$ C、 $- 6$ D、4

查看试题解析
10. 某商场在一次买卖中，同时卖出两件上衣，每件都以150元出售，若按成本计算，其中一件赢利50%，另一件亏本25%，在这次买卖中，该商场（）

A、不盈不亏 B、盈利20元 C、亏损10元 D、盈利50元

查看试题解析
11. 关于 $x$ 的一元一次方程 $2 x^{a - 2} + m = 4$ 的解为 $x = 1$ ，则 $a + m$ 的值为（）

A、9 B、8 C、5 D、4

查看试题解析
12. 将一些形状相同的小棒按如图所示的方式摆放．图①中有3根小棒，图②中有9根小棒，图③中有18根小棒，照此规律，图⑧中小棒的根数为（）

A、84 B、96 C、108 D、118

查看试题解析

二、填空题：（共6小题，每小题2分，共12分）

13. 单项式 $- \frac{2}{3} a^{2} b^{3} c$ 的系数是，次数是次．

查看试题解析
14. 若单项式 $2 x^{2} y^{m}$ 与 $- x^{n} y^{3}$ 是同类项，则 $m + n =$ .

查看试题解析
15. 如图，是一个正方体纸盒的展开图，正方体的各面上标有“知识就是力量”六个字，则原正方体中与“知”字相对的字是．

查看试题解析
16. 如下图是一个数值运算程序，当输入值为 $- 5$ 时，则输出的数值为．

查看试题解析
17. 如图，直线AB ， CD相交于点O ， $O P ⊥ A B$ ， O为垂足，若 $∠ B D C = 14 °$ ，则 $∠ P D O =$ ．

查看试题解析
18. 若规定： $a \otimes b = \frac{a b}{a + b}$ ，则（1） $(- 5) \otimes (- 1) =$ ；（2） $2 \otimes (- 3) \otimes 4 =$

查看试题解析

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

19. 计算： $- 1^{2024} - 6 \times (- \frac{1}{3}) + 2^{2} \div (- 2)$

查看试题解析
20. 读下列语句，并画出图形：
直线m经过A ， B ， C三点，并且点C在点A与B之间，作射线CD ，使 $∠ D C A$ 是锐角．

查看试题解析
21. 已知： $A - 2 B = 8 a^{2} - 8 a b$ ，且 $B = - 4 a^{2} + 5 a b + 6$ ．

(1)、求A等于多少？

(2)、若 $| a - 1 | + (b + 2)^{2} = 0$ ，求A的值．

查看试题解析
22. 为了增强体质，小明给自己设定：以每天跑步 $a$ 千米为基准，超过的部分记为正，不足的部分记为负，手机应用程序统计小明一周跑步情况，记录如下：
星期
一
二
三
四
五
六
日
与基准的差 $/$ 千米
     $+ 0.2$
     $+ 0.8$
     $+ 0.8$
$- 0.4$
$- 0.8$
$+ 1.2$
$+ 0.4$
小明周六和周日共跑了 $21.6$ 千米．

(1)、求 $a$ 的值．

(2)、小明本周共跑了多少千米？

查看试题解析
23. 为了美化环境，某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积．

(1)、甲、乙两工程队每天各能完成多少平方米的绿化改造面积？

(2)、该社区需要进行绿化改造区域共有12000平方米，甲队每天的施工费用为600元，乙队每天的施工费用为400元，比较以下三种方案：①甲队单独完成；②乙队单独完成；③甲、乙两队全程合作完成，哪一种方案的施工费用最少？

查看试题解析
24. 如图，C是线段AB上一点，M是线段AC的中点，N是线段BC的中点.

(1)、如果AB＝20 cm，AM＝6 cm，求NC的长；

(2)、如果MN＝6 cm，求AB的长.

查看试题解析
25. 如图，OC平分 $∠ A O B$ ， OD是 $∠ B O C$ 内部从点O出发的一条射线，OE平分 $∠ A O D$ ．

(1)、【基础尝试】如图2，若 $∠ A O B = 120 °$ ， $∠ C O D = 10 °$ ，求 $∠ D O E$ 的度数；

(2)、【画图探究】设 $∠ C O E = x °$ ，用x的代数式表示 $∠ B O D$ 的度数；

(3)、【拓展运用】若 $∠ C O E$ 与 $∠ B O D$ 互余， $∠ A O B$ 与 $∠ C O D$ 互补，求 $∠ A O B$ 的度数．

查看试题解析
26. 数轴上两点A ， B表示的数分别为a ， b ，其中 $(a + 1)^{2} + | b - 6 | = 0$ ，有一点M位于点B的左侧并与点B的距离是5，点M为线段AC的中点．

(1)、画出数轴，并用数轴上的点表示点A ，点B ，点C ，点M；

(2)、若点P从点O出发，沿数轴以每秒2个单位长度的速度向右匀速移动，设移动时间为t秒．当 $t = 1$ 时，线段PM的长是；此时线段PM与线段PC的数量关系是；

(3)、若点P从点A出发，沿数轴以每秒2个单位长度的速度向右匀速移动，同时点Q从点B出发，沿数轴以每秒1个单位长度的速度向左匀速移动，设移动时间为t秒．当 $P O = 1$ 时，求t的值．

查看试题解析

星期	一	二	三	四	五	六	日
与基准的差 $/$ 千米	$+ 0.2$	$+ 0.8$	$+ 0.8$	$- 0.4$	$- 0.8$	$+ 1.2$	$+ 0.4$