广西壮族自治区柳州市鹿寨县2023-2024学年七年级上学期期末热身卷数学试题
试卷更新日期:2024-01-24 类型:期末考试
一、单选题(共12小题,每小题3分,共36分)
-
1. 下列四个数中,属于负数的是( )A、 B、3.14 C、0 D、22. 据央视6月初报道,电信5G技术赋能千行百业,打造数字经济底座.5G牌照发放三年来,三大电信运营商共投资4772亿元.把数字4772亿用科学记数法表示为( )A、 B、 C、 D、3. 若与是同类项,则的值为( )A、7 B、5 C、3 D、24.
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
 A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、以上都不是5. 某品牌大米包装的质量标识为 , 下列实际质量中不符合标识的是( )A、 B、 C、 D、6. 下列等式变形错误的是A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列说法中,正确的是( )A、 的系数是 B、的系数是 C、的常数项为 D、是四次三项式8. 计算的值为( )A、10 B、 C、 D、119. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|﹣|c﹣b|的结果是( )
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、以上都不是5. 某品牌大米包装的质量标识为 , 下列实际质量中不符合标识的是( )A、 B、 C、 D、6. 下列等式变形错误的是A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列说法中,正确的是( )A、 的系数是 B、的系数是 C、的常数项为 D、是四次三项式8. 计算的值为( )A、10 B、 C、 D、119. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|﹣|c﹣b|的结果是( ) A、a+b B、a+c C、c﹣a D、a+2b﹣c10. 甲仓库存煤吨,乙仓库存煤吨,若甲仓库每天运出吨煤,乙仓库每天运进吨煤,几天后乙 仓库存煤比甲仓库多倍?设天后乙仓库存煤比甲仓库存煤多倍,则有( )A、 B、 C、 D、11. 在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( ).
A、a+b B、a+c C、c﹣a D、a+2b﹣c10. 甲仓库存煤吨,乙仓库存煤吨,若甲仓库每天运出吨煤,乙仓库每天运进吨煤,几天后乙 仓库存煤比甲仓库多倍?设天后乙仓库存煤比甲仓库存煤多倍,则有( )A、 B、 C、 D、11. 在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( ). A、28 B、54 C、65 D、7512. (阅读理解)计算:25×11=275,13×11=143,48×11=528,74×11=814,观察算式,我们发现两位乘11的速算方法:头尾一拉,中间相加,满十进一.[拓展应用]已知一个两位数,十位上的数字是a,个位上的数字是b,这个两位数乘11,计算结果的十位上的数字可表示为( )A、a或a+1 B、a+b或ab C、a+b−10 D、a+b或a+b−10
A、28 B、54 C、65 D、7512. (阅读理解)计算:25×11=275,13×11=143,48×11=528,74×11=814,观察算式,我们发现两位乘11的速算方法:头尾一拉,中间相加,满十进一.[拓展应用]已知一个两位数,十位上的数字是a,个位上的数字是b,这个两位数乘11,计算结果的十位上的数字可表示为( )A、a或a+1 B、a+b或ab C、a+b−10 D、a+b或a+b−10二、填空题(共6小题,每小题2分,共12分)
-
13. 的余角是°.14. 用四舍五入法将精确到 , 所得到的近似数是15. 某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负): , , ,则车上还有人.16. 在一场NBA篮球比赛中,姚明共投中a个2分球,b个3分球,还通过罚球得到9分.在这场比赛中,他一共得了分.17. 把一副三角尺按如图所示拼在一起,其中 , , 三点在同一直线上, 平分 , 平分 ,则 .
 18. 如图,现有一张边长为1的正方形纸片,第1次沿着线段剪开,留下三角形;第2次取的中点 , 再沿着剪开,留下三角形;第3次取的中点 , 再沿着剪开,留下三角形……如此进行下去,在第n次后,被剪去图形的面积之和是 .
18. 如图,现有一张边长为1的正方形纸片,第1次沿着线段剪开,留下三角形;第2次取的中点 , 再沿着剪开,留下三角形;第3次取的中点 , 再沿着剪开,留下三角形……如此进行下去,在第n次后,被剪去图形的面积之和是 .
三、解答题(共7小题,72分)
-
19. 计算:20. 解方程:21. 已知式子 , .(1)、当时,求的值;(2)、若存在一个 , 使的值与的取值无关,求的值.22. “大米小珍馐,小吃大灵魂.粉好度日月,螺小赛乾坤.”广西螺蛳粉日渐成为风靡全国的“舌尖网红”.现有8箱螺蛳粉,称后的纪录如下(单位:千克)

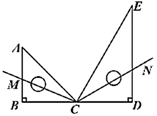
回答下列问题:
(1)、 如果每箱螺蛳粉以4千克为标准,这8箱螺蛳粉中最接近标准重量的是哪一箱?(2)、 以每箱4千克为标准,与标准重量比较,8箱螺蛳粉总计超过或不足多少千克?(3)、若螺蛳粉每千克售价25元,则出售这8箱螺蛳粉可卖多少元?23. 如图,正方形和正方形的边长分别为和6,点、、在一条直线上,点、、在一条直线上,将依次连接、、、所围成的阴影部分的面积记为 .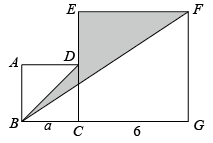 (1)、 试用含的代数式表示;(2)、当时,比较与面积的大小.24. 【阅读理解】规定符号表示两个数中较大的一个.规定符号表示 , 两个数中较小的一个.例如 , . 请计算:的值.(1)、若 , 求的值.(2)、若 , 试求代数式的值.25. 2022年4月23日,我们迎来了第27个世界读书日,邕城校园里也掀起一阵阅读热潮.某校七(1)班以读书日为契机,持续开展系列读书活动,现决定购买甲、乙两种图书共50册,甲种图书每册8元,乙种图书每册10元.(1)、若七(1)班购买这两种图书共用去470元,则甲、乙两种图书各购买多少册?(2)、 同学们经过统计调查发现:甲、乙两种图书的借阅率分别为85%,90%.若要使这批图书的总借阅率不低于87%,甲种图书最多购买多少本?(3)、 若甲种书的单价不变,而乙种书的单价降价10%,这样购买乙种书的总价仍不低于甲种书的总价,则七(1)班至少需要投入多少资金可以完成采购计划?26. 综合与探究(1)、如图1,线段 , 为线段上的一个动点,点 , 分别是 , 的中点.
(1)、 试用含的代数式表示;(2)、当时,比较与面积的大小.24. 【阅读理解】规定符号表示两个数中较大的一个.规定符号表示 , 两个数中较小的一个.例如 , . 请计算:的值.(1)、若 , 求的值.(2)、若 , 试求代数式的值.25. 2022年4月23日,我们迎来了第27个世界读书日,邕城校园里也掀起一阵阅读热潮.某校七(1)班以读书日为契机,持续开展系列读书活动,现决定购买甲、乙两种图书共50册,甲种图书每册8元,乙种图书每册10元.(1)、若七(1)班购买这两种图书共用去470元,则甲、乙两种图书各购买多少册?(2)、 同学们经过统计调查发现:甲、乙两种图书的借阅率分别为85%,90%.若要使这批图书的总借阅率不低于87%,甲种图书最多购买多少本?(3)、 若甲种书的单价不变,而乙种书的单价降价10%,这样购买乙种书的总价仍不低于甲种书的总价,则七(1)班至少需要投入多少资金可以完成采购计划?26. 综合与探究(1)、如图1,线段 , 为线段上的一个动点,点 , 分别是 , 的中点.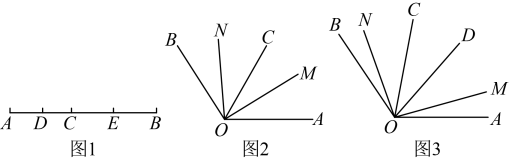
①若 , 则线段的长为;
②设 , 则线段的长为 .(2)、知识迁移:我们发现角的很多规律和线段一样,如图2,若 , 是内部的一条射线,射线平分 , 射线平分 , 求的度数.(3)、已知在内的位置如图3所示,若 , 且 , , 求与的数量关系.