【培优卷】2024年浙教版数学八年级下册5.3 正方形
试卷更新日期:2024-01-24 类型:同步测试
一、选择题
-
1. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )
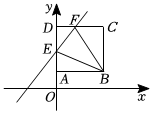 A、 B、 C、 D、2. 如图,正方形的边长为 , 点 , 分别在 , 上,若 , 且 , 则的长为( )
A、 B、 C、 D、2. 如图,正方形的边长为 , 点 , 分别在 , 上,若 , 且 , 则的长为( )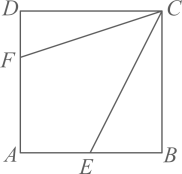 A、 B、 C、 D、3. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )
A、 B、 C、 D、3. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )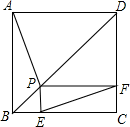 A、2个 B、3个 C、4个 D、5个4. 如图,正方形的边长为 , 点在对角线上,且 , , 垂足为 , 则的长为( )
A、2个 B、3个 C、4个 D、5个4. 如图,正方形的边长为 , 点在对角线上,且 , , 垂足为 , 则的长为( ) A、 B、 C、 D、5. 在菱形ABCD中,M , N , P , Q分别为边AB , BC , CD , DA上的一点(不与端点重合),对于任意的菱形ABCD , 下面四个结论中:
A、 B、 C、 D、5. 在菱形ABCD中,M , N , P , Q分别为边AB , BC , CD , DA上的一点(不与端点重合),对于任意的菱形ABCD , 下面四个结论中:①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形
正确的结论的个数是( )
A、1个 B、2个 C、3个 D、4个6. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )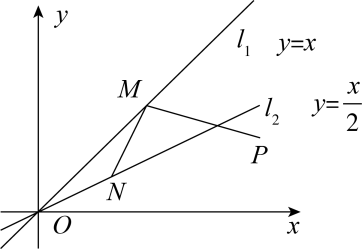 A、2 B、 C、 D、7. 如图,在正方形中,E为对角线AC上一点,连接 , 过点E作 , 交BC延长线于点F,以为邻边作矩形 , 连接 . 在下列结论中:
A、2 B、 C、 D、7. 如图,在正方形中,E为对角线AC上一点,连接 , 过点E作 , 交BC延长线于点F,以为邻边作矩形 , 连接 . 在下列结论中:①;
②;
③;
④ .
其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
 9. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
9. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 . 10. 如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有个
10. 如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有个 11. 如图,正方形 , 点E、F、G、H分别在边上,若与的夹角为 , , , 则的长度为 .
11. 如图,正方形 , 点E、F、G、H分别在边上,若与的夹角为 , , , 则的长度为 . 12. 如图,在四边形中, , , , E是中点,且 , 则线段的长度是 .
12. 如图,在四边形中, , , , E是中点,且 , 则线段的长度是 . 13. 如图,在四边形中, , , , 连接 , , 则以下结论:①;②;③;④ , 其中正确的结论有.(填序号)
13. 如图,在四边形中, , , , 连接 , , 则以下结论:①;②;③;④ , 其中正确的结论有.(填序号)
三、解答题
-
14. 已知正方形 .
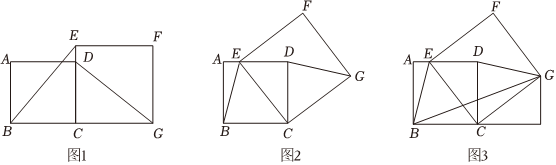 (1)、如图所示,若点在的延长线上,以为一边构造正方形 , 连接和 , 则与的数量关系为 , 位置关系为 .(2)、如图所示,若是边上的一个动点,以为一边在的右侧作正方形 , 连接和请判断线段与有怎样的数量关系和位置关系,并说明理由;(3)、如图所示,在(2)的条件下,连接若 , , 求线段的长.15. 如图,正方形中,点在上(与点不重合),连接 . 将线段绕点逆时针旋转 , 得到线段 , 过点作 , 交延长线于点 .
(1)、如图所示,若点在的延长线上,以为一边构造正方形 , 连接和 , 则与的数量关系为 , 位置关系为 .(2)、如图所示,若是边上的一个动点,以为一边在的右侧作正方形 , 连接和请判断线段与有怎样的数量关系和位置关系,并说明理由;(3)、如图所示,在(2)的条件下,连接若 , , 求线段的长.15. 如图,正方形中,点在上(与点不重合),连接 . 将线段绕点逆时针旋转 , 得到线段 , 过点作 , 交延长线于点 . (1)、依题意补全图形;(2)、连接 , 试判断与的数量关系,并证明.16. 如图,在中, , 过点的直线 , 为上一点,过点作 , 交直线于点 , 垂足为 , 连接 , .
(1)、依题意补全图形;(2)、连接 , 试判断与的数量关系,并证明.16. 如图,在中, , 过点的直线 , 为上一点,过点作 , 交直线于点 , 垂足为 , 连接 , .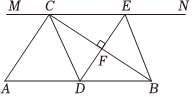 (1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.17. 如图,在平面直角坐标系中,点、点分别在轴与轴上,直线的解析式为 , 以线段、为边作平行四边形 .(1)、如图 , 若点的坐标为 , 判断四边形的形状,并说明理由;(2)、如图 , 在的条件下,为边上的动点,点关于直线的对称点是 , 连接 , .
(1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.17. 如图,在平面直角坐标系中,点、点分别在轴与轴上,直线的解析式为 , 以线段、为边作平行四边形 .(1)、如图 , 若点的坐标为 , 判断四边形的形状,并说明理由;(2)、如图 , 在的条件下,为边上的动点,点关于直线的对称点是 , 连接 , .当 ▲ 时,点位于线段的垂直平分线上;
连接 , , 设 , 设的延长线交边于点 , 当时,求证: , 并求出此时的值.

四、综合题
-
18. 如图,已知直线y=kx+b与直线y=-x-9平行,且y=kx+b还过点(2,3),与y轴交于A点.
 (1)、求A点坐标;(2)、若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)、在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.
(1)、求A点坐标;(2)、若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)、在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.