【提升卷】2024年浙教版数学八年级下册5.3 正方形
试卷更新日期:2024-01-24 类型:同步测试
一、选择题
-
1. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等2. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
 A、2.5 B、 C、 D、23. 下列说法正确的是( )A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形4. 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,下列说法错误的是 ( )
A、2.5 B、 C、 D、23. 下列说法正确的是( )A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形4. 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,下列说法错误的是 ( ) A、若AC⊥BD,四边形ABCD是菱形 B、若AC=BD,四边形ABCD是矩形 C、若AC⊥BD且AC=BD,四边形ABCD是正方形 D、若∠ABC=90°,四边形ABCD是正方形5. 下列命题中,真命题是( ).A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形6. 有下列命题:
A、若AC⊥BD,四边形ABCD是菱形 B、若AC=BD,四边形ABCD是矩形 C、若AC⊥BD且AC=BD,四边形ABCD是正方形 D、若∠ABC=90°,四边形ABCD是正方形5. 下列命题中,真命题是( ).A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形6. 有下列命题:①对角线相等且互相平分的四边形是矩形;②对角线互相垂直的四边形是菱形;③对角线垂直且相等的四边形是正方形;④四边相等的四边形是菱形.其中,真命题有( )个.
A、1 B、2 C、3 D、47. 如图、正方形ABCD的边长为4,G是对角线BD上一动点,于点E , 于点F , 连接EF , 给出四种情况:
①若G为BD的中点,则四边形CEGF是正方形;
②若G为BD上任意一点,则;
③点G在运动过程中,的值为定值4;
④点G在运动过程中,线段EF的最小值为 .
正确的有( )
A、①②③④ B、①②③ C、①②④ D、①③④8. 如图,四边形中, , 边 , 点在边上, , , 则长为( ) A、 B、 C、 D、或
A、 B、 C、 D、或二、填空题
-
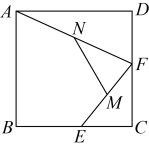
9. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
 10. 如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=
10. 如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE= 11. 如图, , 正方形和正方形的面积分别是169和144,则以为直径的半圆的面积是 .
11. 如图, , 正方形和正方形的面积分别是169和144,则以为直径的半圆的面积是 . 12. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.
12. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.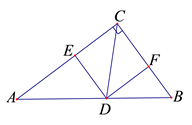 13. 如图, , , , 连接 , 若 , , 则的面积是 .
13. 如图, , , , 连接 , 若 , , 则的面积是 .
三、解答题
-
14. 已知,正方形的四条边相等,四个角是直角.如图,点E,F分别在正方形的两边和上,与相交于点G , 且 .
 (1)、求证:;(2)、若 , 求的长度.15. 在平面直角坐标系中,分别描出点 , , , .
(1)、求证:;(2)、若 , 求的长度.15. 在平面直角坐标系中,分别描出点 , , , .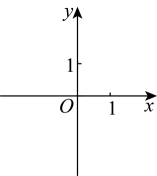 (1)、试判断四边形的形状;(2)、若两点不动,你能通过变动点的位置使四边形成为正方形吗?若能,请写出变动后的点的坐标.16. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,AE⊥AF.
(1)、试判断四边形的形状;(2)、若两点不动,你能通过变动点的位置使四边形成为正方形吗?若能,请写出变动后的点的坐标.16. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,AE⊥AF.求证:四边形AECF是正方形.

四、综合题
-
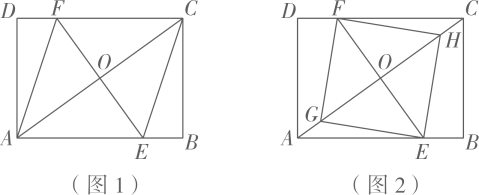
17. 如图1,矩形ABCD中,过对角线AC的中点O画EF⊥AC分别交AB,CD于点E,F,连结AF,CE.
 (1)、[证明体验]
(1)、[证明体验]求证:四边形AECF是菱形.
(2)、[基础巩固]若AB=8,BC=6,求菱形AECF的边长.
(3)、[拓展延伸]如图2,在对角线AC上取点G,H,使得四边形EHFG是正方形,若正方形EHFG的边长为 , 且AE=5CH,求矩形ABCD的面积.