【培优卷】2024年浙教版数学八年级下册5.2 菱形
试卷更新日期:2024-01-23 类型:同步测试
一、选择题
-
1. 如果点A的坐标为 , 点B的坐标为 , 则线段AB中点坐标为 . 这是小白在一本课外书上看到的一种求线段中点坐标的方法,请你利用这种方法解决下面的问题:如图,在平面直角坐标系中,矩形的顶点B的坐标为 , 四边形是菱形,D的坐标为 . 若直线l把矩形和菱形组成的图形的面积分成相等的两部分,则直线l的解析式为( ).
 A、y=2x+11 B、y=-2x+12 C、 D、2. 如图,在矩形中, , 点M、N分别在边上,连接 . 若四边形是菱形,则等于( )
A、y=2x+11 B、y=-2x+12 C、 D、2. 如图,在矩形中, , 点M、N分别在边上,连接 . 若四边形是菱形,则等于( )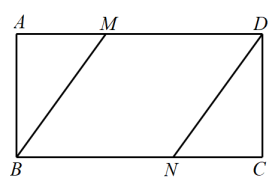 A、 B、 C、 D、3. 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P , 使△PBE的周长最小,则△PBE的周长的最小值为( )
A、 B、 C、 D、3. 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P , 使△PBE的周长最小,则△PBE的周长的最小值为( ) A、2+2 B、4 C、4 D、64. 如图,四边形是菱形, 点M,N是对角线上的三等分点,点P是菱形边上的动点,则满足的点P的个数有( )
A、2+2 B、4 C、4 D、64. 如图,四边形是菱形, 点M,N是对角线上的三等分点,点P是菱形边上的动点,则满足的点P的个数有( ) A、2个 B、4个 C、8个 D、12个5. 如图,在平行四边形中,、分别为边、的中点,是对角线, , 交的延长线于 , 连接 , 若 . 下列结论:①;②四边形是菱形;③;④ . 其中正确的是( )
A、2个 B、4个 C、8个 D、12个5. 如图,在平行四边形中,、分别为边、的中点,是对角线, , 交的延长线于 , 连接 , 若 . 下列结论:①;②四边形是菱形;③;④ . 其中正确的是( ) A、①②③④ B、①②③ C、①②④ D、①③④6. 如图1,在中, , 为钝角.要在对边 , 上分别找点M,N,使四边形为菱形.现有图2中的甲、乙两种用尺规作图确定点M,N的方案,则可得出结论( )
A、①②③④ B、①②③ C、①②④ D、①③④6. 如图1,在中, , 为钝角.要在对边 , 上分别找点M,N,使四边形为菱形.现有图2中的甲、乙两种用尺规作图确定点M,N的方案,则可得出结论( ) A、只有甲正确 B、只有乙正确 C、甲、乙都不正确 D、甲、乙都正确7. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、只有甲正确 B、只有乙正确 C、甲、乙都不正确 D、甲、乙都正确7. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
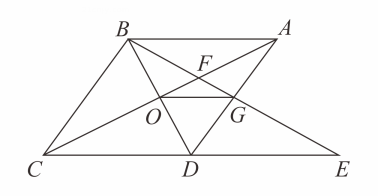
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、二、填空题
-
8. 如图,矩形中,为的中点,过点的直线分别与 , 交于点 , , 连接交于点 , 连接 , 若 , , 则下列结论:
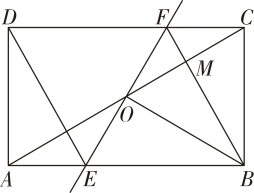
;
;
≌;
四边形是菱形.
其中正确的结论有填写所有正确结论的序号 .
9. 如图,在菱形中, , 与交于点 , 点为延长线上一点,且 , 连接 , 分别交、于点、点 , 连接、 , 则下列结论:
;
四边形是菱形;
四边形与四边形面积相等.
其中正确的结论有个
三、作图题
-
10. 如图,在菱形中,点E在边上,仅用无刻度直尺完成下列画图,保留作图痕迹,不需要写作法.
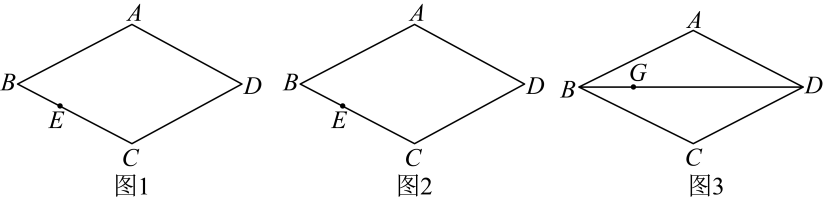 (1)、如图1,在上画点F,使四边形是平行四边形;(2)、如图2,在上画点K,使;(3)、如图3,若点G在上,在上画点H,使四边形是菱形.
(1)、如图1,在上画点F,使四边形是平行四边形;(2)、如图2,在上画点K,使;(3)、如图3,若点G在上,在上画点H,使四边形是菱形.四、解答题
-
11. 在四边形中, , 对角线平分 , 点为边上一点,连接交于点 , .
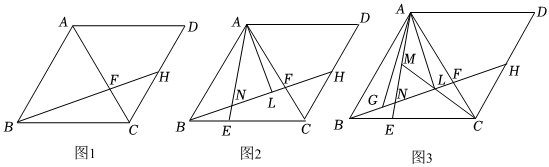 (1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,12. 如图,在四边形中 , 为对角线的中点,过点作直线分别与边 , 交于 , 两点,连接 , .
(1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,12. 如图,在四边形中 , 为对角线的中点,过点作直线分别与边 , 交于 , 两点,连接 , .
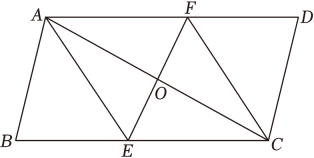 (1)、求证:四边形是平行四边形;(2)、当平分时,
(1)、求证:四边形是平行四边形;(2)、当平分时,①试说明四边形是菱形;
②当四边形是矩形时,若 , , 求的长.
13. 在矩形中, , , , 是对角线上的两个动点,分别从 , 同时出发相向而行,速度均为 , 运动时间为秒,当其中一个动点到达后就停止运动. (1)、若 , 分别是 , 中点,求证:四边形始终是平行四边形.(2)、在(1)条件下,当为何值时,四边形为矩形.(3)、若 , 分别是折线 , 上的动点,与 , 相同的速度同时出发,当为何值时,四边形为菱形.
(1)、若 , 分别是 , 中点,求证:四边形始终是平行四边形.(2)、在(1)条件下,当为何值时,四边形为矩形.(3)、若 , 分别是折线 , 上的动点,与 , 相同的速度同时出发,当为何值时,四边形为菱形.五、综合题
-
14. 如图 , 四边形为菱形, . , , .
 (1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.
(1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.求证: , 并求的最小值;
点在线段上运动时,点的横坐标是否发生变化?若不变,请求出点的横坐标若变化,请说明理由.
15. 已知:如图,四边形是矩形,分别延长 , 到点E,F,使 , , 连接 . (1)、求证:四边形是菱形;(2)、连接 , 如果四边形的周长是 , , 求的长.
(1)、求证:四边形是菱形;(2)、连接 , 如果四边形的周长是 , , 求的长.
-

