【提升卷】2024年浙教版数学八年级下册5.1 矩形
试卷更新日期:2024-01-23 类型:同步测试
一、选择题
-
1. 如图,在矩形中,对角线与相交于点 , 已知 , 则的大小是( )
 A、 B、 C、 D、2. 如图,在矩形中,平分交于点E,连接 , 若 , 则的长为( )
A、 B、 C、 D、2. 如图,在矩形中,平分交于点E,连接 , 若 , 则的长为( ) A、12 B、14 C、16 D、203. 在四边形ABCD中, , .下列说法能使四边形ABCD为矩形的是( )A、 B、 C、 D、4. 如图所示,在正方形中,是对角线上一点,过作 , , 垂足分别为、 , 连接 , 若 , 则的长为( )
A、12 B、14 C、16 D、203. 在四边形ABCD中, , .下列说法能使四边形ABCD为矩形的是( )A、 B、 C、 D、4. 如图所示,在正方形中,是对角线上一点,过作 , , 垂足分别为、 , 连接 , 若 , 则的长为( )
 A、 B、 C、 D、5. 下列关于矩形的说法,正确的是( ).A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分
A、 B、 C、 D、5. 下列关于矩形的说法,正确的是( ).A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分二、填空题
-
6. 矩形ABCD中,M为对角线BD的中点,点N在边AD上,且 . 当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .7. 如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为.
 8. 如图,在四边形 中, , ,在不添加任何辅助线的前提下,要想四边形 成为一个矩形,只需添加的一个条件是.
8. 如图,在四边形 中, , ,在不添加任何辅助线的前提下,要想四边形 成为一个矩形,只需添加的一个条件是.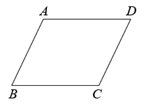 9. 如图1是某学校食堂墙壁上“光盘行动,从我做起”的长方形宣传画,画的左侧为一个圆盘上摆放一双筷子,画的下边缘为水平线,图2是其示意图,水平线l上的点A在圆心O的正下方,筷子与右下方交于B,C两点,线段 , 分别垂直l于点D,E.测得 , , 则圆盘的半径为.
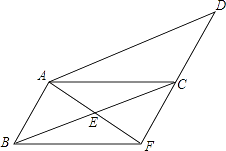
9. 如图1是某学校食堂墙壁上“光盘行动,从我做起”的长方形宣传画,画的左侧为一个圆盘上摆放一双筷子,画的下边缘为水平线,图2是其示意图,水平线l上的点A在圆心O的正下方,筷子与右下方交于B,C两点,线段 , 分别垂直l于点D,E.测得 , , 则圆盘的半径为. 10. 如图,AC平分∠BAD,AB∥CD, BC=4, ∠BAD=30°,∠B=90° ,则CD的长为 .
10. 如图,AC平分∠BAD,AB∥CD, BC=4, ∠BAD=30°,∠B=90° ,则CD的长为 .
三、解答题
-
11. 如图,将矩形绕点旋转得到矩形 , 点在上,连接.
 (1)、求证:平分;(2)、连接交于点 , 点是的中点,连接、 , 若 , 求的长.12. 如图,在▱中,平分 , 平分 , , .
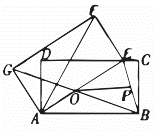
(1)、求证:平分;(2)、连接交于点 , 点是的中点,连接、 , 若 , 求的长.12. 如图,在▱中,平分 , 平分 , , . (1)、求证:四边形是矩形;(2)、若点恰好在上,且 , 设的周长为 , 的周长为 , , 求常数的值.13. 如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
(1)、求证:四边形是矩形;(2)、若点恰好在上,且 , 设的周长为 , 的周长为 , , 求常数的值.13. 如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.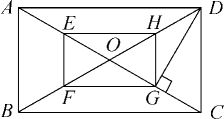 (1)、求证:四边形EFGH是矩形;(2)、若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.14. 如图,在▱中,对角线 , 相交于点 , 于点 , 于点 , .
(1)、求证:四边形EFGH是矩形;(2)、若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.14. 如图,在▱中,对角线 , 相交于点 , 于点 , 于点 , .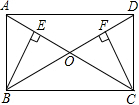 (1)、求证:▱是矩形.(2)、若 , , 求的长.
(1)、求证:▱是矩形.(2)、若 , , 求的长.四、综合题