【培优卷】2024年浙教版数学八年级下册4.6 反证法
试卷更新日期：2024-01-23 类型：同步测试
一、选择题
-
1. 用反证法证明命题“四边形中至少有一个角是钝角或直角”时应假设（ ）A、四边形中没有一个角是钝角或直角 B、四边形中至多有一个角是钝角或直角 C、四边形中每一个角都是钝角或直角 D、四边形中至少有一个角是锐角2. 如图，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC.当用反证法证明时，第一步应假设（ ）
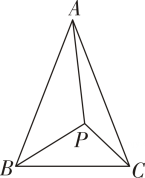A、AB≠AC B、PB=PC C、∠APB=∠APC D、∠ABC≠∠ACB3. 用反证法证明命题“如图，如果 AB∥CD，AB ∥EF，那么CD∥EF”时，第一步是（ ）
A、假设 AB不平行于CD B、假设 AB不平行于 EF C、假设 CD∥EF D、假设 CD不平行于 EF4. 已知命题“在△ABC中，若AB=AC，则∠B<90°”.下面写出运用反证法证明这个命题的四个打乱顺序的步骤：①∴∠A+∠B+∠C>180°，这与三角形内角和为 180°矛盾.
②因此假设不成立，∴∠B<90°.
③假设在△ABC中，∠B≥90°.
④由 AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°.
这四个步骤正确的顺序应是（ ）
A、④③①② B、③④②① C、①②③④ D、③④①②5. 下列说法，错误的是（ ）A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 ， 则”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于”，先假设这个三角形中有一个内角大于60°二、填空题
-
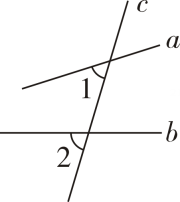
6. 如图，直线a，b被 c 所截，∠1，∠2 是同位角，且∠1≠∠2.求证：a不平行于b.
证明：假设 ， 则 ，这与相矛盾，所以不成立，所以a 不平行于b.
7. 已知命题“在△ABC中，若AC2+BC2≠AB2 ， 则∠C≠90°”，用反证法，其步骤为：假设 ， 根据 ， 一定有 ， 但这与已知相矛盾，因此假设是错误的，故原命题是真命题。8. 用反证法证明（填空）：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行。
已知：如图，直线l1 ， l2被l3所截，∠1+∠2=180°.
求证：l1l2.
证明：假设l1l2 ， 即l1与l2相交于一点P.
则∠1+∠2+∠P180°（）。
所以∠1+∠2180°，这与矛盾，故不成立，
所以。
9. 如图①，我们想要证明“如果直线AB，CD被直线EF所截，AB∥CD，那么∠EOB=∠EO'D．”如图②，假设∠EOB≠∠EO'D，过点O作直线A'B'，使∠EOB'=∠EO'D，可得A'B'∥CD．这样过点O就有两条直线AB，A'B’都平行于直线CD，这与基本事实““矛盾，说明∠EOB≠∠EO'D的假设是不对的，于是有∠EOB=∠EO'D．
三、解答题
-
10. 已知 x3+bx2+cx+d 的系数都是整数．若bd+cd为奇数，求证：这个多项式不能表示为两个整系数的多项式的乘积．
11. 平面上有8条直线两两相交．试证明在所有的交角中至少有一个角小于23°．
12. 如图，直线a、b、c在同一平面内，以a∥b，a与c相交于点P，试说明b与c也一定相交．
13. 7条直线两两相交，试证明：在所有的交角中，至少有一个角小于26°．
14. 用反证法证明：一个三角形中不能有两个角是直角．已知： ， ， 是的三个内角．
求证： ， ， 中不能有两个角是直角．
15. 阅读材料：怎样证实“两直线平行，同位角相等”本节中，我们用叠合的方法发现了“两直线平行，同位角相等” .事实上，这个结论可以运用已有的基本事实，通过说理加以证实.
如图，直线AB、CD被直线EF所截，AB//CD，∠1与∠2是同位角.
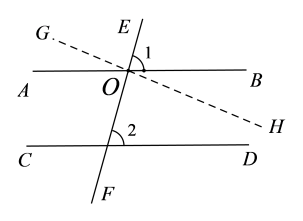
假设∠1∠2，那么可以通过直线AB与EF的交点O作直线GH，使∠EOH=∠2，直线GH与直线AB是两条直线.
根据基本事实“同位角相等，两直线平行”，由∠EOH=∠2，可以得到GH//CD.
这样，过点O就有两条直线AB、GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.
这说明∠1∠2的假设不正确，于是∠1=∠2.
解决问题：若且 ， 请你用以上方法说明：.
16. 阅读下列文字，回答问题.题目：在Rt△ABC中，∠C=90°，若∠A≠45°，所以AC≠BC．
证明：假设AC=BC，∵∠A≠45°，∠C=90°，∴∠A≠∠B，∴AC≠BC．这与假设矛盾，所以AC≠BC．
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正.
