【提升卷】2024年浙教版数学八年级下册4.6 反证法
试卷更新日期:2024-01-23 类型:同步测试
一、选择题
-
1. 用反证法证明“三角形的三个外角中至多有一个锐角”,应先假设( )A、三角形的三个外角都是锐角 B、三角形的三个外角中至少有两个锐角 C、三角形的三个外角中没有锐角 D、三角形的三个外角中至少有一个锐角2. 用反证法证明“在中,若 , 则”时,则应假设( )A、 B、 C、 D、3. 用反证法证明:“在同一平面内,若 , , 则”时,首先应假设( )A、 B、 C、a与b相交 D、a与c相交4. 用反证法证明命题:“在中,对边是 , 若 , 则”的第一步应假设( )A、 B、 C、 D、5. 选择用反证法证明“已知:在中,求证: , 中至少有一个角不大于”时,应先假设( )A、 , B、 , C、 , D、 ,
二、填空题
-
6. 用反证法证明“已知五个正数的和等于1,求证:这五个正数中至少有一个大于或等于 ”时,首先要假设.7. 对于命题“如图,如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形”.用反证法证明这个结论时,第一步应假设 .
 8. 要用反证法证明等腰三角形的底角必为锐角,应先假设 .9. 用反证法证明:一个三角形中至少有一个角不小于60°,应先假设 .10. 用反证法证明某一命题的结论“ ”时,应假设.
8. 要用反证法证明等腰三角形的底角必为锐角,应先假设 .9. 用反证法证明:一个三角形中至少有一个角不小于60°,应先假设 .10. 用反证法证明某一命题的结论“ ”时,应假设.三、解答题
-
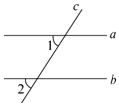
11. 用反证法证明:等腰三角形的底角必定是锐角.12. 已知:如图,直线a,b被c所截,∠1,∠2是同位角,且∠1≠∠2.
求证:a不平行于b.