【提升卷】2024年浙教版数学八年级下册4.5 三角形的中位线
试卷更新日期:2024-01-23 类型:同步测试
一、选择题
-
1. 如图, 已知在 中, 是 A C边上的中线,按下列步骤作图:①分别以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相交于点M,N:②过点M,N作直线MN,分别交BC,BE于点D,O:③连接CO,DE.则下列结论错误的是( )
 A、OB=OC B、 C、 D、2. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、OB=OC B、 C、 D、2. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )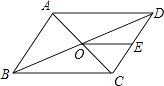 A、15 B、18 C、21 D、243. 如图,已知在△ABC中,∠ABC'<90°,AB≠BC,BE是AC边上的中线.按下列步骤作图:①分別以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相父于点M,N:②过点M,N作直线MN,分别交BC,BE于点D,O;③连接CO,DE.则下列结论错误的是( )
A、15 B、18 C、21 D、243. 如图,已知在△ABC中,∠ABC'<90°,AB≠BC,BE是AC边上的中线.按下列步骤作图:①分別以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相父于点M,N:②过点M,N作直线MN,分别交BC,BE于点D,O;③连接CO,DE.则下列结论错误的是( ) A、OB=OC. B、∠BOD=∠COD C、DE∥AB D、DB=DE4. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( )
A、OB=OC. B、∠BOD=∠COD C、DE∥AB D、DB=DE4. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( ) A、1 B、2 C、3 D、45. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为( )
A、1 B、2 C、3 D、45. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为( )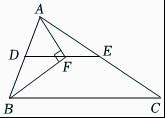 A、 B、 C、 D、6. 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=2,△AOE的周长为10,则平行四边形ABCD的周长为( )
A、 B、 C、 D、6. 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=2,△AOE的周长为10,则平行四边形ABCD的周长为( ) A、16 B、32 C、36 D、407. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )
A、16 B、32 C、36 D、407. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )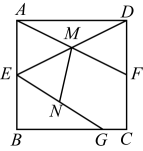 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
8. 如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为 .
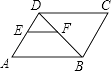 9. 如图,点D,E,F分别是的边 , , 的中点,如果 , 那么等于 .
9. 如图,点D,E,F分别是的边 , , 的中点,如果 , 那么等于 . 10. 如图,在中,D、E分别是AB、AC的中点,则 .
10. 如图,在中,D、E分别是AB、AC的中点,则 . 11. 如图,平行四边形的对角线与相交于点 , 且 , 若是边的中点, , , 则的长为 .
11. 如图,平行四边形的对角线与相交于点 , 且 , 若是边的中点, , , 则的长为 .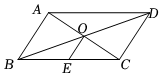 12. 如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=10,DM=2,则AB等于
12. 如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AC=10,DM=2,则AB等于 13. 在Rt△ABC中,∠C=90°,AC=5,BC=12,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN'的中点,则DE的最小值是
13. 在Rt△ABC中,∠C=90°,AC=5,BC=12,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN'的中点,则DE的最小值是
三、解答题
-
14. 在中, , 点E、F分别是BC,AC的中点,延长BA到点D,使 , 连接DE,DF、AE,EF,DE与AF交于点O.
 (1)、求证:AF与DE互相平分;(2)、若 , . 请直接写出DE的长为 .
(1)、求证:AF与DE互相平分;(2)、若 , . 请直接写出DE的长为 .四、实践探究题
-
15. 综合与实践

【问题情境】
如图1,有两张等腰三角形纸片ABC和AEF,其中AB=AC,AE=AF,∠BAC+∠EAF=180°.△AEF绕着A顺时针旋转,旋转角为(),点M为BF的中点.
【特例感知】
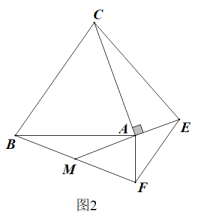
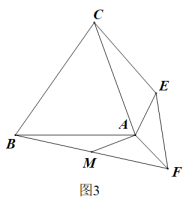
(1)、如图1,当时,AM和CE的数量关系是;(2)、如图2,当时,连接AM,CE,请判断AM和CE的数量关系,并说明理由;(3)、【深入探究】如图3,当为任意锐角时,连接AM,CE,则(2)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
-