【培优卷】2024年浙教版数学八年级下册4.2 平行四边形
试卷更新日期:2024-01-23 类型:同步测试
一、选择题
-
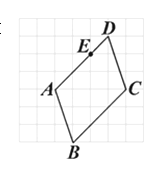
1. 如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )
 A、
A、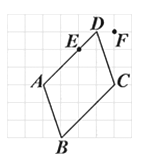 B、
B、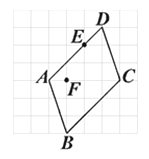 C、
C、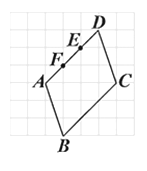 D、
D、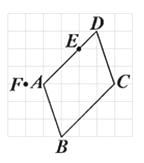 2. 如图, 方格纸中小正方形的边长为1, , 两点在格点上,要在图中格点上找到点 ,使得 的面积为2,满足条件的点 有( )
2. 如图, 方格纸中小正方形的边长为1, , 两点在格点上,要在图中格点上找到点 ,使得 的面积为2,满足条件的点 有( )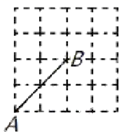 A、无数个 B、7个 C、6个 D、5个3. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )
A、无数个 B、7个 C、6个 D、5个3. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )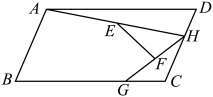 A、 B、 C、 D、24. 如图,▱ABCD的对角线AC、BD交于点O , AE平分∠BAD交BC于点E , 且
A、 B、 C、 D、24. 如图,▱ABCD的对角线AC、BD交于点O , AE平分∠BAD交BC于点E , 且∠ADC=60° , AB=BC , 连接OE.下列结论:①AE>CE;②S▱ABCD=AB·AC;③S△ABE=2S△AOE;④OE=AD , 其中成立的有 ( )
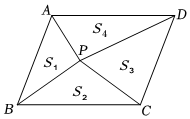
 A、1个 B、2个 C、3个 D、4个5. 如图,点 是▱ 内的任意一点,连接 、 、 、 ,得到 、 、 、 ,设它们的面积分别是 、 、 、 ,给出如下结论中正确的是( )
A、1个 B、2个 C、3个 D、4个5. 如图,点 是▱ 内的任意一点,连接 、 、 、 ,得到 、 、 、 ,设它们的面积分别是 、 、 、 ,给出如下结论中正确的是( ); 如果 ,则 ; 若 ,则 ; 如果 点在对角线 上,则 : : ; 若 ,则 点一定在对角线 上.
 A、 B、 C、 D、6. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或7. 如图,中, , 于F,交于E,若 , 则的大小是( )
A、 B、 C、 D、6. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或7. 如图,中, , 于F,交于E,若 , 则的大小是( ) A、 B、 C、 D、8. 如图,在▱ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则▱ABCD的面积为( )
A、 B、 C、 D、8. 如图,在▱ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则▱ABCD的面积为( )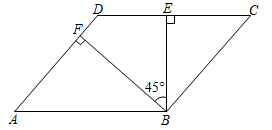 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 两条平行线间的距离公式
一般地;两条平行线l1:Ax+By+C1=0和l2:Ax+By+C2=0间的距离公式是d= 如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
解:将两方程中x,y的系数化成对应相等的形式,得2x+6y﹣8=0和2x+6y﹣9=0,因此,d= 两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 .
10. 在中, , , , 为外的一点,且 . 若点到边上的最短距离记为 , 当绕旋转时,的取值范围是 . 11. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .
11. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .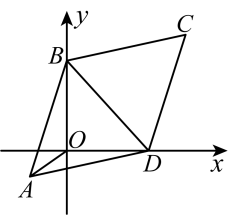 12. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为.
12. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为. 13. 如图,矩形的边、上有两点、 , 沿着直线折叠使得点、分别落在、 , 交线段于点 , 射线恰好经过点 , 作平分交于 , , 且恰好落在线段的延长线上,若 , 则到直线的距离是 .
13. 如图,矩形的边、上有两点、 , 沿着直线折叠使得点、分别落在、 , 交线段于点 , 射线恰好经过点 , 作平分交于 , , 且恰好落在线段的延长线上,若 , 则到直线的距离是 .
三、作图题
-
14. 如图,平行四边形中, , 请仅用无刻度的直尺完成下列作图(要求:①不写作法,②保留作图痕迹,③说明作图结果.):
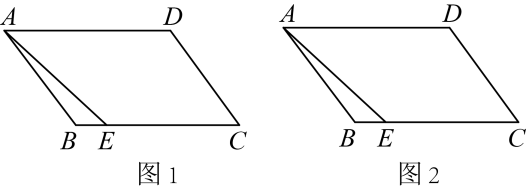 (1)、在图1中,作出的角平分线;(2)、在图2中,作出的角平分线.
(1)、在图1中,作出的角平分线;(2)、在图2中,作出的角平分线.四、解答题
-
15. 已知点和直线 , 则点P到直线的距离可用公式计算.
例如:求点到直线的距离.
解:∵直线 , 其中 , .
∴点到直线的距离为: .
根据以上材料,解答下列问题:
(1)、求点到直线:的距离;(2)、直线:沿y轴向上平移2个单位得到直线 , 求、这两条平行直线之间的距离.16. 如图,直线:与直线:交于点 , 与轴交于点 , 与轴交于点 .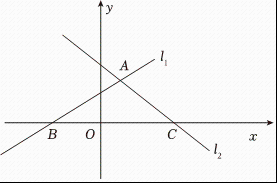 (1)、求直线和直线的表达式;(2)、点是轴上一点,点是直线上一点,以点、、、为顶点的四边形是平行四边形,且 , 求点的坐标.17. 如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)、求直线和直线的表达式;(2)、点是轴上一点,点是直线上一点,以点、、、为顶点的四边形是平行四边形,且 , 求点的坐标.17. 如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.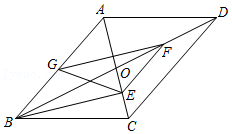 (1)、求证:∠OBE=∠ADO;(2)、若F、G分别是OD、AB的中点,且BC= ,
(1)、求证:∠OBE=∠ADO;(2)、若F、G分别是OD、AB的中点,且BC= ,①求证:△EFG是等腰三角形;
②当EF⊥EG时,求▱ABCD的面积.
五、综合题
-
18. 如图

如图1,已知直线m∥n,点A,B在直线n上,点C,P在直线m上。
(1)、写出图1中面积相等的各对三角形:。(2)、如图1,A,B,C为三个顶点,点P在直线m上移动到任一位置时,总有与△ABC的面积相等。(3)、如图2,一个五边形ABCDE,你能否过点E作一条直线交BC(或BC的延长线)于点M,使四边形ABME的面积等于五边形ABCDE的面积?19. 我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”. (1)、如图1,试说明直线AE是“好线”的理由;(2)、如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并说明理由;(3)、如图3,五边形ABCDE是一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但原块土地与开垦荒地的分界小路(折线CDE)还保留着,现在请你过E点修一条直路.要求直路左边的土地面积与原来一样多(只需对作图适当说明无需说明理由)20. 如图,在中, , , , 点P沿AB边从点A开始以2cm秒的速度向点B移动,同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动,用t表示移动的时间 .
(1)、如图1,试说明直线AE是“好线”的理由;(2)、如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并说明理由;(3)、如图3,五边形ABCDE是一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但原块土地与开垦荒地的分界小路(折线CDE)还保留着,现在请你过E点修一条直路.要求直路左边的土地面积与原来一样多(只需对作图适当说明无需说明理由)20. 如图,在中, , , , 点P沿AB边从点A开始以2cm秒的速度向点B移动,同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动,用t表示移动的时间 . (1)、当t为何值时,△PAQ是等边三角形.(2)、当t为何值时,△PAQ为直角三角形.21. 如图,在平行四边形中, , 点E为边上一点,连结交对角线于点F.(1)、如图,若 , , 求的长度;
(1)、当t为何值时,△PAQ是等边三角形.(2)、当t为何值时,△PAQ为直角三角形.21. 如图,在平行四边形中, , 点E为边上一点,连结交对角线于点F.(1)、如图,若 , , 求的长度;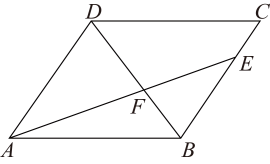 (2)、如图,若 , 点G,H为边的两点,连接 , , , 且满足 . 求证: .
(2)、如图,若 , 点G,H为边的两点,连接 , , , 且满足 . 求证: .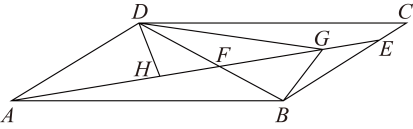 (3)、如图,若 , , 将沿射线方向平移,得到 , 连接 , , 当的值最小时,请直接写出的最小值.
(3)、如图,若 , , 将沿射线方向平移,得到 , 连接 , , 当的值最小时,请直接写出的最小值.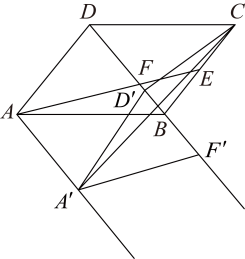 22. 如图1,在平行四边形ABCD中,∠B为锐角,AB=AD,点P,H分别在边AD、CB上,且DP=BH,连接PH交对角线AC于点F:
22. 如图1,在平行四边形ABCD中,∠B为锐角,AB=AD,点P,H分别在边AD、CB上,且DP=BH,连接PH交对角线AC于点F:
 (1)、请说明AF与FC的大小关系,并说明理由(2)、如图2,在AB边上取点M、N (点N在BM之间)使AM=5BN.点P从点D匀速运动到点A时,点Q恰好从点M匀速到点N,连接PQ交对角线AC于点E,记QM=x,AP=y,已知y=-2x+12,请分别求出AD,BN的长.
(1)、请说明AF与FC的大小关系,并说明理由(2)、如图2,在AB边上取点M、N (点N在BM之间)使AM=5BN.点P从点D匀速运动到点A时,点Q恰好从点M匀速到点N,连接PQ交对角线AC于点E,记QM=x,AP=y,已知y=-2x+12,请分别求出AD,BN的长. (3)、如图3,在第(2)题的条件下,连接QF,QH,若∠B=60°,则△FQH面积的最小值为(请直接写出答案),
(3)、如图3,在第(2)题的条件下,连接QF,QH,若∠B=60°,则△FQH面积的最小值为(请直接写出答案),
-