【培优卷】2024年浙教版数学八年级下册4.3 中心对称

试卷更新日期：2024-01-23 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，线段 $a^{'}$ 是由线段a经过平移得到的，线段 $a^{'}$ 还可以看作是线段a经过怎样的图形变化得到？下列结论：①1次中心对称；②1次轴对称；③2次轴对称．其中所有正确结论的序号是（）　　

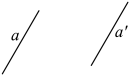A、①② B、②③ C、①③ D、①②③

查看试题解析
2. 图甲和图乙中所有的小正方形都全等，将图甲的正方形放在图乙中①、②、③、④的某个位置，使它与原来7个小正方形组成的图形是中心对称图形．这个位置是（）

A、① B、② C、③ D、④

查看试题解析
3. 如图，在平面直角坐标系 $x O y$ 中， $△ A B C$ 经过中心对称变换得到 $△ A^{'} B^{'} C^{'}$ ，那么中心对称的坐标为（）．

A、 $(0 ， 0)$ B、 $(- 1 ， 0)$ C、 $(- 1 ， - 1)$ D、 $(0 ， - 1)$

查看试题解析
4. 如图，在正方形网格中，A，B，C，D，E，F，G，H，I，J是网格线交点， $△ A B C$ 与 $△ D E F$ 关于某点成中心对称，则其对称中心是（）

A、点G B、点H C、点I D、点J

查看试题解析
5. 如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（）

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题

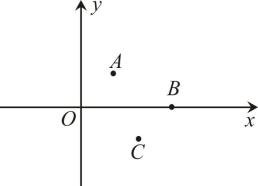
6. 如图，在平面直角坐标系中，点A，B，C的坐标分别为 $(1 ， 1)$ ， $(3 ， 0)$ ， $(2 ， - 1)$ ．点M从坐标原点O出发，第一次跳跃到点 $M_{1}$ ，使得点 $M_{1}$ 与点O关于点A成中心对称；第二次跳跃到点 $M_{2}$ ，使得点 $M_{2}$ 与点 $M_{1}$ 关于点B成中心对称；第三次跳跃到点 $M_{3}$ ，使得点 $M_{3}$ 与点 $M_{2}$ 关于点C成中心对称；第四次跳跃到点 $M_{4}$ ，使得点 $M_{4}$ 与点 $M_{3}$ 关于点A成中心对称；…，依此方式跳跃，点 $M_{2022}$ 的坐标是．

查看试题解析
7. 如图，已知 AB=3，AC=1，∠D=90°，△DEC 与△ABC关于点C成中心对称，则AE的长是．

查看试题解析
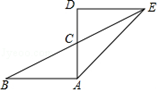8. 如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB＝3，OD＝2，则阴影部分的面积之和为．

查看试题解析
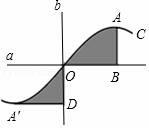9. 如图，直线EF经过平行四边形ABCD的对称中心O，若AE=2 cm，四边形AEFB的面积为12 cm² ，则CF= ，四边形ABCD的面积为.

查看试题解析

三、作图题

10. 如图所示，在平面直角坐标系中，△ABC的三个顶点分别是A（﹣2，﹣2）、B（﹣4，﹣1）、C（﹣4，﹣4）．

(1)、画出△ABC关于原点O或中心对称的△A₁B₁C₁；

(2)、作出点A关于x轴的对称点A′，若把点A′向右平移a个单位长度后落在△A₁B₁C₁的内部（不包括顶点和边）．
①在图中画出点A′，并写出点A′坐标．
②写出a的取值范围为．

查看试题解析
11. 如图是由边长为1的小等边三角形构成的网格，点A和点B均在格点上．

(1)、在图①中画出以AB为边的四边形ABCD，要求该四边形是中心对称图形，但不是轴对称图形，且点C和点D均在格点上（画出一个即可）；

(2)、在图②中画出以AB为边的四边形ABEF，要求该四边形既是中心对称图形，又是轴对称图形，且点E和点F均在格点上（画出一个即可）．

查看试题解析
12. 如图，在 $4 \times 4$ 正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为 $1 .$ 点 $A$ 、 $B$ 都在格点上，按下列要求作图，使得所画图形的顶点均在格点上．

(1)、在图 $1$ 中以线段 $A B$ 为边画一个等腰三角形 $A B C$ ；

(2)、在图 $2$ 中以线段 $A B$ 为边画一个轴对称的四边形 $A B D E$ ；

(3)、在图 $3$ 中以线段 $A B$ 为边画一个中心对称的四边形 $A B F G$ ，使其面积为 $4$ ．

查看试题解析
13. 在 $4 \times 4$ 的方格中，选择 $6$ 个小方格涂上阴影，请仔细观察图 $1$ 中的六个图案的对称性，按要求回答．

(1)、请在六个图案中，选出三个具有相同对称性的图案．
选出的三个图案是 $($ 填写序号 $)$ ；
它们都是图形 $($ 填写“中心对称”或“轴对称” $)$ ；

(2)、请在图2中，将1个小方格涂上阴影，使整个 $4 \times 4$ 的方格也具有(1)中所选图案相同的对称性．

查看试题解析
14. 如图，方格纸中每个小正方形的边长均为1个单位长度， $△ A B C$ 的顶点、点D和线段EF的端点均在小正方形的顶点上．

(1)、在方格纸中画出 $△ A B C$ 关于点D成中心对称的 $△ M N P$ （点A的对称点是点M，点B的对称点是点N，点C的对称点是点P），点M、N、P在小正方形的顶点上；

(2)、在方格纸中画出以EF为斜边的 $R t △ E F G$ ，且 $t a n ∠ G F E = 2$ ，点G在小正方形的顶点上．连接NG，请直接写出线段NG的长．

查看试题解析

四、综合题

15. 如图，在平面直角坐标系中，线段AB的两个端点坐标分别为 $A (- 4 ， 3)$ ， $B (- 1 ， 2)$ ．

(1)、若将线段AB经过一次平移后得到对应线段 $A_{1} B_{1}$ ，点 $A_{1}$ 的坐标为 $(1 ， 2)$ ，请直接写出点 $B_{1}$ 的坐标；并直接写出线段AB上的点 $P (a ， b)$ 的对应点 $P_{1}$ 的坐标（用含a，b的代数式表示）（不需要在答题卡上画图）；

(2)、直接写出（1）中线段AB经过一次平移得到线段 $A_{1} B_{1}$ 的平移距离；

(3)、若在平面直角坐标系中线段AB关于原点O成中心对称的线段是 $A_{2} B_{2}$ ，请直接写出点 $B_{2}$ 的坐标（不需要在答题卡上画图）

查看试题解析
16.

(1)、如图，四边形ABCD是李爷爷家的一块平行四边形田地，P为水井，现要把这块田地平均分给他的两个儿子，为了方便用水，要求两个儿子分到的地都与水井相邻，请你来设计一下，并说明你的理由。

(2)、规律总结：回顾第13题和第14题第（1）问发现：能够平分平行四边形面积与周长的直线有条，它们的共同特点是经过的交点。

查看试题解析
17. 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为 $A (1 ， 1)$ ， $B (3 ， 4)$ ， $C (4 ， 0)$ ．

(1)、请调出将△ABC向左平移4个单位长度，再向上平移1个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、请画出与△ABC关于原点对称的 $△ A_{2} B_{2} C_{2}$ ；

(3)、直接写出 $B_{1}$ ， $B_{2}$ 两点的坐标．

查看试题解析
18. 已知Rt△ABC，AB＝AC，点D在△ABC的外部，且∠DAC＜90°，

(1)、如图1，若AD＝AC，求∠BDC；

(2)、如图2，点E在线段AC上，线段DE的垂直平分线交BC的延长线于点P.当点D正好和点B关于线段AC的中点对称时，
①证明：△PDE为直角三角形；

②连接BE、AD，若 $\frac{S_{△ B E C}}{S_{△ B E P}} = \frac{8}{11}$ ，直接写出 $\frac{S_{△ A D E}}{S_{△ P C E}}$ ＝.

查看试题解析
19.
对于坐标平面内的点，现将该点向右平移1个单位，再向上平移2的单位，这种点的运动称为点A的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5），已知点A的坐标为（1，0）．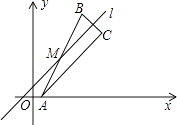

(1)、分别写出点A经1次，2次斜平移后得到的点的坐标．

(2)、如图，点M是直线l上的一点，点A关于点M的对称点的点B，点B关于直线l的对称轴为点C．
①若A、B、C三点不在同一条直线上，判断△ABC是否是直角三角形？请说明理由．
②若点B由点A经n次斜平移后得到，且点C的坐标为（7，6），求出点B的坐标及n的值．

查看试题解析
20. 知识背景：
过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.

(1)、如图1，直线m 经过▱ABCD对角线的交点 O，则 $S_{四边形 A E F B}$ $S_{四边形 D E F C}$ (填“〉”“〈”或“=”).

(2)、将两个正方形按如图2 所示的方式摆放，O为小正方形对角线的交点，作过点 O 且将整个图形分成面积相等的两部分的直线.

(3)、将8个大小相同的正方形按如图3 所示的方式摆放，作将整个图形分成面积相等的两部分的直线（用三种不同的方法）.

查看试题解析