【提升卷】2024年浙教版数学八年级下册4.2 平行四边形

试卷更新日期：2024-01-23 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，l₁∥l₂∥l₃ ，且相邻两条直线间的距离都是2，A，B，C分别为l₁ ， l₂ ， l₃上的动点，连结AB ，AC，BC，AC与l₂交于点D，∠ABC= 90°，则BD的最小值为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 如图，直线AB∥CD，GH平分∠CGF，GI平分∠DGF，且HG＝15cm，GI＝20cm，HI＝25cm，则直线AB与直线CD之间的距离是（）

A、10cm B、12cm C、13cm D、14cm

查看试题解析
3. 在同一平面内，已知 $a ∥ b ∥ c$ ，若直线a、b之间的距离为 $7 c m$ ，直线b、c之间的距离为 $3 c m$ ，则直线a、c间的距离为（）

A、 $4 c m$ 或 $10 c m$ B、 $4 c m$ C、 $10 c m$ D、不确定

查看试题解析
4. 在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（）

A、22 B、20 C、22或20 D、18

查看试题解析
5. 如图，▱ABCD的对角线AC、BD交于点O，▱ABCD的周长为30，直线EF过点O，且与AD，BC分别交于点E．F，若OE＝5，则四边形ABFE的周长是（）

A、30 B、25 C、20 D、15

查看试题解析
6. 如图，在平行四边形 $A B C D$ 中， $A D = 2 A B$ ， $F$ 是 $A D$ 的中点，作 $C E ⊥ A B$ ，垂足 $E$ 在线段 $A B$ 上，连接 $E F$ 、 $C F$ ，则下列结论： $(1) ∠ D C F = \frac{1}{2} ∠ B C D$ ； $(2) E F = C F$ ； $(3) S_{△ B E C} = 2 S_{△ C E F}$ ； $(4) ∠ D F E = 3 ∠ A E F .$ 其中正确的结论是（）

A、 $(1) (2)$ B、 $(1) (2) (4)$ C、 $(2) (3) (4)$ D、 $(1) (3) (4)$

查看试题解析

二、填空题

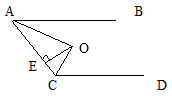
7. 如图所示，AB//CD，O为∠A、∠C的平分线的交点O，OE⊥AC于E，且OE=2，则AB与CD之间的距离等于.

查看试题解析
8. 如图，三角形材料ABC ， ∠B＝90°，BC＝4，AC＝5，点D在边BC上，添加一块三角形材料ACE ，加工成 $▱$ ADCE的材料，则 $▱$ ADCE的对角线DE的最小值是．

查看试题解析
9. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(1 ， 0)$ ，点 $B$ 的坐标为 $(4 ， 0)$ ，点 $C$ 在 $y$ 轴的正半轴上，且 $O B = 2 O C$ ，在平面直角坐标系内确定点 $D$ ，使得以点 $D ， A ， B ， C$ 为顶点的四边形是平行四边形，则点 $D$ 的坐标为．

查看试题解析
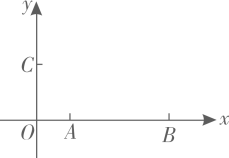10. 在同一平面内，有相互平行的三条直线a，b，c，且a，b之间的距离为1，b，c之间的距离是2，若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上，如图所示，∠BAC＝90°，在△ABC的面积是.

查看试题解析
11. 如图所示，在平行四边形 $A B C D$ 中，以 $A$ 为圆心， $A B$ 长为半径画弧交 $A D$ 于点 $F$ ，再分别以点 $B$ 、 $F$ 为圆心，大于 $\frac{1}{2} B F$ 为半径画弧，两弧交于一点 $P$ ，连接 $A P$ 交 $B C$ 于点 $E$ ，连接 $E F .$ 若 $B F = 6$ ， $A B = 5$ ，则四边形 $A B E F$ 的面积为．

查看试题解析

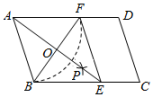
三、作图题

12. 如图，已知 $△ A B C$ ，根据下列要求画图并回答问题：

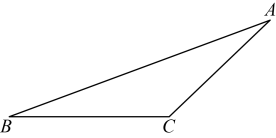(1)、画 $B C$ 边上的高 $A H$ ，过点 $C$ 画直线 $C D ∥ A B$ ，交 $A H$ 于点 $D$ ；（不要求写画法和结论）

(2)、在（1）的图形中，如果 $A B = 7$ ， $B C = 4$ ， $A H = \sqrt{6}$ ，求直线 $A B$ 与 $C D$ 间的距离．

查看试题解析
13. 如图，每个小正方形的边长都是1， $A$ ， $B$ ， $C$ ， $D$ 均在网格的格点上．

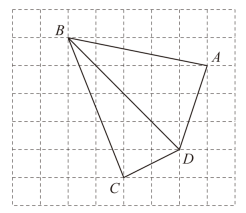(1)、判断 $∠ B C D$ 是否为直角：．（填写“是”或“不是”）

(2)、直接写出四边形 $A B C D$ 的面积为．

(3)、找到格点 $E$ ，并画出四边形 $A B E D$ （一个即可），使得其面积与四边形 $A B C D$ 面积相等．

查看试题解析

四、解答题

14. 如图，已知 $▱ A B C D$ 的对角线 $A C$ ， $B D$ 交于点O， $E F$ 过点O且与 $A B$ ， $C D$ 分别相交于点E、F．

(1)、求证： $O E = O F$ ；

(2)、若 $∠ F E B = 90 °$ ， $B E = 15$ ， $B D = 34$ ，求 $E F$ 的长．

查看试题解析
15. 如图，在平面直角坐标系中，四边形ABCD是平行四边形，A(-3，0)，B(3，0) ，C(0，4)，连结OD，点E是线段0D的中点．

(1)、求点E和点D的坐标．

(2)、平面内是否存在一点N，使以C，D，E，N为顶点的四边形是平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析
16. 如图①，在平行四边形ABCD中， AB=3，AD=6．动点P沿AD边以每秒 $\frac{1}{2}$ 个单位长度的速度从点A向终点D ．设点P运动的时间为t（t＞0）秒．

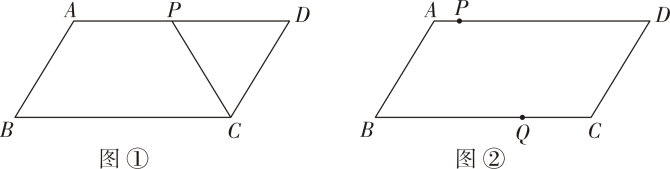(1)、线段PD的长为（用含t的代数式表示）．

(2)、当CP平分∠BCD时，求t的值．

(3)、如图②，另一动点Q以每秒2个单位长度的速度从点C出发，在CB上往返运动．P、Q两点同时出发，点Q也随之停止运动．当以P、D、Q、B为顶点的四边形是平行四边形时，直接写出t的值．

查看试题解析