【提升卷】2024年浙教版数学八年级下册4.1 多边形
试卷更新日期：2024-01-22 类型：同步测试
一、选择题
-
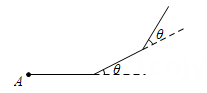
1. 一个多边形的每一个内角都等于140°，那么从这个多边形的一个顶点出发的对角线的条数是（ ）A、6条 B、7条 C、8条 D、9条2. 一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（ ）A、360° B、540° C、720° D、900°3. 一个多边形剪去一个角后得到一个新的多边形，则关于这两个多边形，下列量中一定没有发生变化的是（ ）A、内角度数 B、内角和度数 C、对角线条数 D、外角和度数4. 从一个多边形的一个顶点出发，最多可画条对角线，则它是（ ）边形．A、 B、 C、 D、5. 小丽利用最近学习的数学知识，给同伴出了这样一道题：如图，小刚从点 A 出发，沿直线走 6米后向左转θ，接着沿直线前进 6 米后，再向左转θ……如此下去，当他第一次回到点A时，发现自己走了 72米，则θ的度数为（ ）
A、28° B、30° C、33° D、36°6. 如图，在正六边形内作正方形 ， 连接 ， 则等于（ ）
A、 B、 C、 D、二、填空题
-
7. 一个多边形所有的内角与它所有的外角之和是 ， 过这个多边形的一个顶点可画出条对角线．8. 如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=69°，则∠5=°.
9. 一个多边形的内角和跟它的外角和相等，则这个多边形是边形．10. 如图，M是△ABC两个内角平分线的交点，N是△ABC两个外角平分线的交点，设∠BMC=α，∠BNC=β，则α+β=°.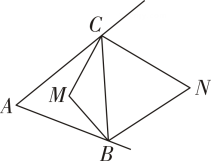
11. 已知一个多边形被截取一个角后，内角和变为 ， 则原多边形的边数为.12. 如图，蜂巢的横截面由正六边形组成，且能无限无缝隙拼接，称横截面图形由全等正多边形组成，且能无限无缝隙拼接的多边形具有同形结构．若已知具有同形结构的正n边形的每个内角度数为α，满足：360=kα（k为正整数），多边形外角和为360°，则k关于边数n的函数是（写出n的取值范围）
13. 如图，边形 ， 从边形的一个顶点出发可以作条对角线．若过边形的一个顶点有7条对角线，边形没有对角线，边形对角线的总条数等于边数，则 ．三、解答题
-
14. 在学习多边形的相关知识时，小张同学和小王同学对老师布置“探究多边形的对角线条数”的作业很感兴趣，小张同学探究得到了边形的对角线条数的公式，并通过上网查证自己探究的结论是正确的．下图是两位同学进行交流的情景．小王同学把哪个多边形对角线的条数数错了？请你通过计算或者画图来说明．
15. 已知一个正多边形的边数为n．(1)、若这个多边形的内角和为其外角和的4倍，求n的值．(2)、若这个正多边形的一个内角为 ， 求n的值，16. 如图，佳佳从点出发，前进10米后向右转 ， 再前进10米后又向右转 ， 如此反复下去，直到他第一次回到出发点 ， 他所走的路径构成了一个多边形．
(1)、佳佳一共走了多少米？(2)、求这个多边形的内角和．17.
(1)、用一条直线去截多边形，使得到的新多边形分别满足下列条件(在对应的图中画出图形，把截去的部分打上阴影)：①在图1中，新多边形的内角和比原多边形的内角和增加了 180°.
②在图2中，新多边形的内角和与原多边形的内角和相等.
③在图3中，新多边形的内角和比原多边形的内角和减少了 180°.
(2)、若将一个多边形截去一个角后，得到的新多边形的内角和为 2 520°，求原多边形的边数.18. 探究归纳题：
(1)、试验分析：如图1，经过A点可以作条对角线；同样，经过B点可以作条；经过C点可以作条；经过D点可以作条对角线.
通过以上分析和总结，图1共有条对角线.
(2)、拓展延伸：运用（1）的分析方法，可得：
图2共有条对角线；
图3共有条对角线；
(3)、探索归纳：对于n边形(n>3)，共有条对角线．(用含n的式子表示)
(4)、特例验证：十边形有条对角线.