吉林省长春市汽开九中2023-2024学年八年级上学期期中考试试卷

试卷更新日期：2024-01-22 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共24分）

1. 若分式 $\frac{1}{x - 3}$ 有意义，则x满足的条件是（　　）

A、x＝3 B、x＜3 C、x＞3 D、x≠3

查看试题解析
2. 每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为0.0000108m ，该数值用科学记数法表示为（　　）

A、1.08×10^﹣4 B、1.08×10^﹣5 C、﹣1.08×10⁵ D、108×10^﹣6

查看试题解析
3. 已知一个等腰三角形的两边长分别是4，5，则它的周长是（）

A、13 B、14 C、13或14 D、9或12

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，则 $A B$ 的长为（）

A、5 B、10 C、 $2 \sqrt{7}$ D、28

查看试题解析
5. 下列运算正确的是（　　）

A、a²•a³＝a⁵ B、（ab）²＝ab² C、（a^﹣3）²＝a^﹣9 D、（π﹣3.14）⁰＝π﹣3.14

查看试题解析
6. 如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是（）．

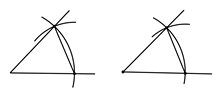A、SAS B、ASA C、AAS D、SSS

查看试题解析
7. 白日登山望烽火，黄昏饮马傍交河．诗中隐含着一个有趣的数学问题：诗中将军在观望烽火之后从山脚上的A点出发，奔向小河旁边的P点饮马，饮马后再到B点宿营，若A、B到水平直线l（l表示小河）的距离分别是2，1，AB两点之间水平距离是4，则AP+PB最小值为（　　）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图，直线a，b相交形成的夹角中，锐角为52°，交点为O，点A在直线a上，直线b上存在点B，使以点O，A，B为顶点的三角形是等腰三角形，这样的点B有（　　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共18分）

9. 分解因式：a²﹣a= ．

查看试题解析
10. 如图， $△ A B C ≌ △ F D E$ ， $A B = F D ， B C = D E ， A E = 20 c m ， F C = 10 c m$ ，则 $A F$ 的长是 $c m$ ．

查看试题解析
11. 将直线 $y = 3 x$ 向下平移2个单位长度，得到直线的解析式为．

查看试题解析
12. 在平面直角坐标系xOy中，若点（1，y₁），（4，y₂）在一次函数y＝kx+b（k＞0）的图象上，则y₁y₂（填“＞”，“＝”或“＜”）．

查看试题解析
13. 如图，已知函数y＝﹣x+b与函数y＝kx+7的图象交于点P（﹣2，3），则关于x的不等式﹣x+b≤kx+7的解集是．

查看试题解析
14. 如图，将长方形ABCD沿对角线AC翻折，点B落在点F处，FC交AD于点E，若AB=4，BC＝8，则△ACE的面积为．

查看试题解析

三、解答题（共78分）

15.

(1)、先化简，再求值： $\frac{2 a}{a^{2} - 16} - \frac{1}{a + 4}$ ，其中a＝2．

(2)、解方程： $\frac{x + 2}{x - 1} = \frac{3}{x - 1}$ ．

查看试题解析
16. 在社区全民健身活动中，父子俩参加跳绳比赛．相同时间内父亲跳180个，儿子跳210个．已知儿子每分钟比父亲多跳20个，父亲、儿子每分钟各跳多少个？

查看试题解析
17. 如图，已知∠C=∠D，∠CAB=∠DAB.
求证：BC=BD

查看试题解析
18. 如图，强大的台风使得一根旗杆在离地面3m处折断倒下，旗杆顶部落在离旗杆底部4m处，旗杆折断之前有多高？

查看试题解析

19. 教育部印发的《义务教育课程方案》和《课程标准》（2022年版）将劳动从原来的综合活动课中独立出来．某中学为了解学生做家务的情况，随机抽取了若干学生进行了问卷调查，并将数据整理后，绘制成如下不完整的统计图：

调查问卷

在下列家务劳动中①整理房间，打扫卫生；②吃过饭后收拾餐桌，洗刷餐具；③清洗自己的衣服，整理衣柜；④给家里的花草浇水施肥或给小动物喂食洗澡，你每周能主动参与做 ____件事情．

A ．零 B ．一 C ．二 D ．三 E ．四

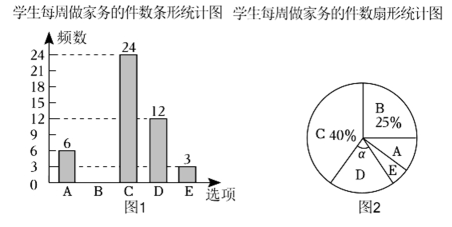
根据图中信息，请完成下列问题：

(1)、本次抽样调查的总人数有人；

(2)、选择B选项的人数有人；

(3)、并补全条形统计图；

(4)、在扇形统计图中，若选项D所对应的圆心角为α，则α＝°；

(5)、若规定“每周能主动做三件家务劳动及以上者”为“优秀家务小能手”，已知该校共有学生1800人，请你估计该校能评为“优秀家务小能手”的学生有人．

查看试题解析

20. 按要求在下列边长为1的小正方形拼成的网格中作图，使点P在格点上．且格点P位置不相同．（每问作出一种情况即可）

(1)、在图1网格中找格点P ，使得AP与AB垂直．

(2)、在图2网格中画线段PA ，使得PA＝AB ．

(3)、在图3网格中画△ABP ，使得△ABP的面积是3．

查看试题解析
21. 密闭容器内有一定质量的气体，当容器的体积V（单位：m³）变化时，气体的密度ρ（单位：kg/m³）随之变化．已知密度ρ与体积V是反比例函数关系，它的图象如图所示．

(1)、求密度ρ关于体积V的函数解析式．

(2)、当V＝8m³时，求该气体的密度ρ．

查看试题解析
22. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
小明和小亮相约到公园游玩 $.$ 已知小明家，小亮家到公园的距离相同，小明先骑车 $6 m i n$ 到达超市，购买了一些食物和饮用水，然后再骑车 $10 m i n$ 到达公园，小明出发 $10 m i n$ 后，小亮骑车从家出发直接到达公园，给出的图象中 $($ 单位： $m)$ 反映了这个过程中小明骑行的路程，请根据相关信息，解答下列问题：

(1)、填表：
小明离开家的时间 $/ m i n$
     $4$
          $6$
          $20$
          $31$
小明骑行的路程 $/ m$

          $1500$

(2)、填空：
$①$ 小明购物的超市到公园的距离是 $m$ ；
$②$ 小亮骑车的速度为 $m / m i n$ ；
$③$ 在小明和小亮从各自的家到公园的途中，当两人到公园的距离相同时，小明离开家的时间为 $m i n$ ；
$④$ 当小亮到达公园时，小明距公园还有 $m .$

(3)、当 $0 \leq x \leq 31$ 时，请直接写出 $y_{1}$ 关于 $x$ 的函数解析式．

查看试题解析
23. 在等腰Rt△ABC中，∠ABC＝90°，点D是射线AB上的动点，AE垂直于直线CD于点E ，交直线BC于点F ．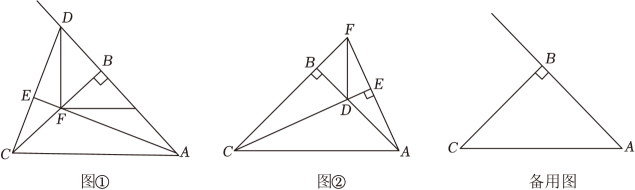

(1)、【探索发现】
如图①，若点D在AB的延长线上，点E在线段CD上时，请猜想CF ， BD ， AB之间的数量关系为；

(2)、【拓展提升】
如图②，若点D在线段AB上（不与点A ， B重合），试猜想CF ， BD ， AB之间的数量关系，并说明理由；

(3)、【灵活应用】
当AB＝3， $C F = 3 \sqrt{2}$ 时，直接写出线段BD的长为．

查看试题解析
24. 在平面直角坐标系中，直线L：y＝kx+b（k≠0）经过点A（﹣2，3），交y轴于点B（0，1）．

(1)、求直线l所对应的函数表达式．

(2)、若点C是y轴上一点，连结AC ．当△ABC的面积为5时，求点C的坐标．

(3)、已知线段MN的端点坐标分别为M(m-1，2)、N( $\frac{1}{2}$ m+3，2)．则当直线l与线段MN有交点时，求m的取值范围．

查看试题解析

小明离开家的时间 $/ m i n$	$4$	$6$	$20$	$31$
小明骑行的路程 $/ m$		$1500$