湖南省邵阳市新邵县2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2024-01-22 类型：期中考试

进入出卷网下载

一、选择题（本大题有10个小题，每小题3分，共30分,在每小题给出的四个选项中只有一项是符合题目要求的）

1. 计算 $(\frac{1}{3})^{- 2}$ 的结果是（）

A、-9 B、9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
2. 下列各式中，正确的是（）

A、 $\frac{a + m}{b + m} = \frac{a}{b}$ B、 $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x + y}$ C、 $\frac{a + b}{a + b} = 0$ D、 $\frac{a b - 1}{a c - 1} = \frac{b - 1}{c - 1}$

查看试题解析
3. 小丽在化简分式 $\frac{*}{x^{2} - 1} = \frac{x - 1}{x + 1}$ 时，*部分不小心滴上了墨水，请你推测，*部分的式子应该是（）

A、 $x^{2} - 2 x + 1$ B、 $x^{2} + 2 x + 1$ C、 $x^{2} - 1$ D、 $x^{2} - 2 x - 1$

查看试题解析
4. 如果一个分式的分子或分母可以因式分解，且这个分式是最简分式，那么我们称这个分式为“和谐分式”．下列分式中，是“和谐分式”的是（）（填序号即可）．
$① \frac{x - 1}{x^{2} + 1} ； ② \frac{a - 2 b}{a^{2} - b^{2}} ； ③ \frac{x + y}{x^{2} - y^{2}} ； ④ \frac{a^{2} - b^{2}}{{(a + b)}^{2}} .$

A、① B、② C、③ D、④

查看试题解析
5. 给出下列4个命题：①相等的角是对顶角；②垂直于同一直线的两条直线平行；③两个锐角的和是钝角；④平行于同一直线的两条直线平行，其中真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，若x为正整数，则表示分式 $\frac{x^{2} + 2 x}{(x + 2) (x + 1)}$ 的值落在（）

A、线①处 B、线②处 C、线③处 D、线④处

查看试题解析
7. 阅读，正如一束阳光．孩子们无论在哪儿，都可以感受到阳光的照耀，都可以通过阅读触及更广阔的世界．某区教育体育局向全区中小学生推出“童心读书会”的分享活动．甲、乙两同学分别从距离活动地点800米和400米的两地同时出发，参加分享活动．甲同学的速度是乙同学的速度的1.2倍，乙同学比甲同学提前4分钟到达活动地点．若设乙同学的速度是x米/分，则下列方程正确的是（）

A、 $\frac{x}{800} - \frac{1.2 x}{400} = 4$ B、 $\frac{1.2 x}{800} - \frac{x}{400} = 4$ C、 $\frac{400}{1.2 x} - \frac{800}{x} = 4$ D、 $\frac{800}{1.2 x} - \frac{400}{x} = 4$

查看试题解析
8. 若某三角形的三边长分别为3，4，m，则m的值可以是（）

A、1 B、5 C、7 D、9

查看试题解析
9. 如图，在△ABC中，AC的垂直平分线交BC于点D ，交AC于点E ， ∠B＝∠ADB ．若AB＝4，则DC的长是（）．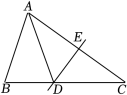

A、2 B、3 C、4 D、不能确定

查看试题解析
10. 如图，△ABC中，D点在BC上，且BD的中垂线与AB相交于E点，CD的中垂线与AC相交于F点，已知△ABC的三个内角皆不相等，根据图中标示的角，判断下列叙述何者正确（）

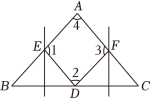A、∠1＝∠3，∠2＝∠4 B、∠1＝∠3，∠2≠∠4 C、∠1≠∠3，∠2＝∠4 D、∠1≠∠3，∠2≠∠4

查看试题解析

二、填空题（本大题有8个小题，每小题3分，共24分）

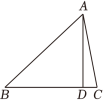
11. 某种细胞的直径是0.00000095米，将0.00000095米用科学记数法表示为．

查看试题解析
12. 观察下列分式，探究其规律： $\frac{x^{4}}{y} ， \frac{x^{7}}{y^{2}} ， \frac{x^{10}}{y^{3}} ， \frac{x^{13}}{y^{4}} ， . . . . . . .$ ，按照上述规律，第n个分式是．

查看试题解析
13. 若 $\frac{b}{a}$ ＝ $\frac{1}{3}$ ，则分式 $\frac{a}{a - b}$ 的值为.

查看试题解析
14. 定义一种新运算 $\int_{\dot{b}}^{a} n x^{n - 1} d x = a^{n} - b^{n}$ ，例如 $\int_{m}^{k} 2 x d x = k^{2} - m^{2}$ ．则 $\int_{2}^{4} - x^{- 2} d x =$ ．

查看试题解析
15. 清初数学家梅文鼎在著作《平三角举要》中，对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明，证明过程中创造性地设计直角三角形，得出了一个结论：如图，AD是锐角△ABC的高，则BD $= \frac{1}{2}$ （BC $+ \frac{A B^{2} - A C^{2}}{B C}$ ）．当AB＝7，BC＝6，AC＝5时，CD＝．

查看试题解析
16. 如图，等边三角形 $A B C$ 的边长为 $6 c m$ ，动点P从点A出发以 $2 c m / s$ 的速度沿 $A B$ 向点B匀速运动，过点P作 $P Q ⊥ A B$ ，交边 $A C$ 于点Q，以 $P Q$ 为边作等边三角形 $P Q D$ ，使点A，D在 $P Q$ 异侧，当点D落在 $B C$ 边上时，点P需移动s．

查看试题解析
17. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC ，点D为BC上一点，连接AD ．过点B作BE⊥AD于点E ，过点C作CF⊥AD交AD的延长线于点F ．若BE＝4，CF＝1，则EF的长度为．

查看试题解析
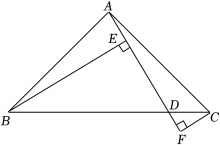18. 如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=6，点F是线段AD上的动点，则BF+EF的最小值为．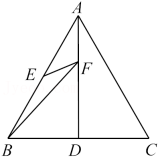

查看试题解析

三、解答题

19. 计算：

(1)、 $(- \frac{1}{2})^{- 1} - 2^{5} \div 2^{3} + {(π - 3.14 + 2020)}^{0}$ ；

(2)、 $\frac{x - y}{x} \div (x + \frac{y^{2} - 2 x y}{x})$ ．

查看试题解析
20. 先化简，再求值：（ $\frac{1}{x - 1} +$ 1） $\div \frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ，其中x＝3．

查看试题解析
21. 解方程：

(1)、 $\frac{3}{x - 1} =$ 5 $+ \frac{3 x}{1 - x}$ ．

(2)、 $\frac{5}{x^{2} + x} - \frac{1}{x^{2} - x} =$ 0．

查看试题解析
22. 某商店以固定进价一次性购进一种商品，3月份按一定售价销售，销售额为2400元，为扩大销量，减少库存，4月份在3月份售价基础上打9折销售，结果销售量增加30件，销售额增加1056元．求该商店3月份这种商品的售价是多少元？

查看试题解析
23. 如图，在△ABC中，AB＝AC ，点D、E都在边BC上，且BE＝CD ，求证：AD＝AE ．

查看试题解析
24. 综合与实践：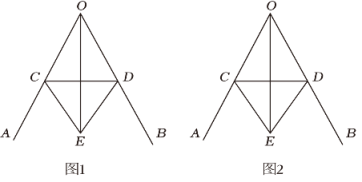

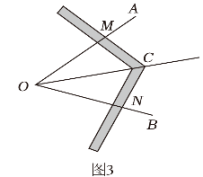(1)、问题探究：如图1是古希腊数学家欧几里得所着的《几何原本》第1卷命题9“平分一个已知角，”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA和OB上分别取点C和D ，使得OC＝OD ，连接CD ，以CD为边作等边三角形CDE ，则OE就是∠AOB的平分线．请写出OE平分∠AOB的依据：；

(2)、类比迁移：小明根据以上信息研究发现：△CDE不一定必须是等边三角形，只需CE＝DE即可，他查阅资料；我国古代已经用角尺平分任意角，做法如下：如图3，在∠AOB的边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同刻度分别与点M ， N重合，则过角尺顶点C的射线OC是∠AOB的平分线，请说明此做法的理由；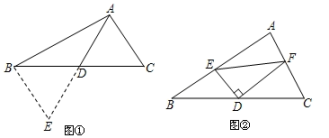

查看试题解析
25.

(1)、方法呈现：
如图①：在△ABC中，若AB=6，AC=4，点D为BC边的中点，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE ，可证△ACD≌△EBD ，从而把AB、AC ， 2AD集中在△ABE中，利用三角形三边的关系即可判断中线AD的取值范围是，这种解决问题的方法我们称为倍长中线法；

(2)、探究应用：如图②，在△ABC中，点D是BC的中点，DE⊥DF于点D ， DE交AB于点E ， DF交AC于点F ，连接EF ，判断BE+CF与EF的大小关系并证明；

(3)、问题拓展：如图③，在四边形ABCD中，AB∥CD ， AF与DC的延长线交于点F、点E是BC的中点，若AE是∠BAF的角平分线．试探究线段AB ， AF ， CF之间的数量关系，并加以证明．

查看试题解析