山东省青岛市黄岛区、胶州市2023-2024学年八年级上学期期中数学试卷
试卷更新日期:2024-01-22 类型:期中考试
一、选择题(本大题共8小题,每小题3分,共24分)在每个题给出的四个选项中,只有一项是符合题目要求的.
-
1. 的倒数是( )A、 B、 C、﹣ D、﹣2. 如图是由边长为的方砖铺设的地板示意图,如果小球在地板上从点滚动到点 , 则小球滚动的最短路程是( )
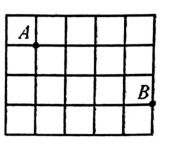 A、 B、 C、 D、3. 在平面直角坐标系内有一点P(x , y),若点P位于第二象限,并且点P到x轴和y轴的距离分别为5,2,则点P的坐标是( )A、(5,2) B、(2,5) C、(2,﹣5) D、(﹣2,5)4. 若一次函数y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上的是( )A、(2,1) B、(2,3) C、(﹣1,1) D、(1,5)5. 下列说法正确的是( )A、0.2是0.4的算术平方根 B、﹣5是25的平方根 C、的算术平方根是9 D、16的平方根是46. 如图,在平面直角坐标系中,△ABC与△A'B'C'关于x轴对称,其中点A , B , C的对应点分别为点A',B',C',若点P(2,3)在△ABC的边上,则点P在△A'B'C'上的对应点P'的坐标是( )
A、 B、 C、 D、3. 在平面直角坐标系内有一点P(x , y),若点P位于第二象限,并且点P到x轴和y轴的距离分别为5,2,则点P的坐标是( )A、(5,2) B、(2,5) C、(2,﹣5) D、(﹣2,5)4. 若一次函数y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上的是( )A、(2,1) B、(2,3) C、(﹣1,1) D、(1,5)5. 下列说法正确的是( )A、0.2是0.4的算术平方根 B、﹣5是25的平方根 C、的算术平方根是9 D、16的平方根是46. 如图,在平面直角坐标系中,△ABC与△A'B'C'关于x轴对称,其中点A , B , C的对应点分别为点A',B',C',若点P(2,3)在△ABC的边上,则点P在△A'B'C'上的对应点P'的坐标是( )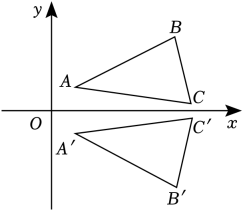 A、(3,2) B、(﹣2,3) C、(2,﹣3) D、(﹣2,﹣3)7. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A、(3,2) B、(﹣2,3) C、(2,﹣3) D、(﹣2,﹣3)7. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )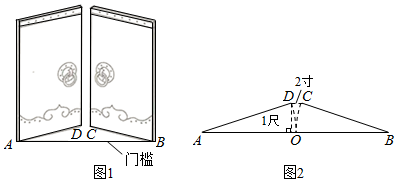 A、50.5寸 B、52寸 C、101寸 D、104寸8. 对于一次函数y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的是( )
A、50.5寸 B、52寸 C、101寸 D、104寸8. 对于一次函数y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的是( ) A、y随x的增大而增大 B、函数图象与y轴的交点位于x轴下方 C、k﹣b<0 D、k+b>0
A、y随x的增大而增大 B、函数图象与y轴的交点位于x轴下方 C、k﹣b<0 D、k+b>0二、填空题(本大题共8小题,每小题3分,共24分)
-
9. 的相反数是 .10. 已知一次函数y=kx+3(k≠0),其函数值y随x值的增大而增大.当x=﹣2时,函数值y可以是 (请写出一个你认为正确的即可).11. 如图,正方形的面积为12,则与该正方形的边长最接近的整数是 .
 12. 已知一次函数y=ax﹣5的图象经过点A(﹣4,3),则关于x的一元一次方程ax﹣5=3的解为 .13. 如图,在四边形中, , 分别以四边形的四条边为边长,向外作四个正方形,面积分别为 . 若 , 则的值为 .
12. 已知一次函数y=ax﹣5的图象经过点A(﹣4,3),则关于x的一元一次方程ax﹣5=3的解为 .13. 如图,在四边形中, , 分别以四边形的四条边为边长,向外作四个正方形,面积分别为 . 若 , 则的值为 .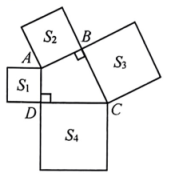 14. 在同一直角坐标系中,直线与轴,轴分别交于两点,直线与轴,轴分别交于两点.若 , 点在点的下方,并且 , 则直线的表达式为 .15. 如图,在直角坐标系中,长方形OABC的顶点A , C分别在x轴,y轴上,点A , C的坐标分别为(﹣7,0),(0,4).E为边BC上一点,点D的坐标为(﹣5,0),若△ODE是腰长为5的等腰三角形,则点E的坐标是 .
14. 在同一直角坐标系中,直线与轴,轴分别交于两点,直线与轴,轴分别交于两点.若 , 点在点的下方,并且 , 则直线的表达式为 .15. 如图,在直角坐标系中,长方形OABC的顶点A , C分别在x轴,y轴上,点A , C的坐标分别为(﹣7,0),(0,4).E为边BC上一点,点D的坐标为(﹣5,0),若△ODE是腰长为5的等腰三角形,则点E的坐标是 .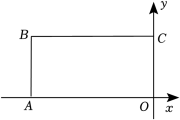 16. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , 则内部的格点个数是 .
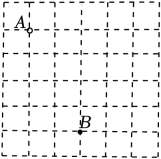
16. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , 则内部的格点个数是 .
三、解答题(本大题共8小题,共72分)
-
17. 计算(1)、(2)、(3)、(4)、18. 围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有4000多年的历史.如图是某围棋棋盘的一部分,若棋盘是由边长均为1的小正方形组成的,棋盘上A , B两颗棋子的坐标分别为A(﹣2,3),B(0,﹣1).
⑴根据题意,画出相应的平面直角坐标系;
⑵有一颗黑色棋子C的坐标为(2,2),请标注出黑色棋子C的位置.
19. 把下列各数写入相应的集合中: , 2.5, , , 0, , , 0.5757757775…(相邻两个5之间7的个数逐次加1).(1)、有理数集合:{ …};(2)、无理数集合:{ …}.20. 党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许多城市再现绿水青山.某小区物业在小区拐角清理出了一块空地进行绿化改造,如图, , .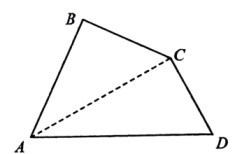 (1)、为了方便居民的生活,在绿化时将修一条从点直通点的小路,求小路的长度;(2)、若该空地的改造费用为每平方米150元,试计算改造这片空地共需花费多少元?21. 我们知道是无理数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
(1)、为了方便居民的生活,在绿化时将修一条从点直通点的小路,求小路的长度;(2)、若该空地的改造费用为每平方米150元,试计算改造这片空地共需花费多少元?21. 我们知道是无理数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如: , 即 , 所以的整数部分为2,小数部分为 .
请根据以上信息,回答下列问题:
(1)、整数部分是 , 小数部分是;(2)、如果的整数部分为的整数部分为 , 求的立方根;(3)、已知 , 其中是整数,且 , 求的值.22. 在平面直角坐标系中,A , B两点的坐标分别是A(0,a),B(0,b),且+|12﹣b|=0.(1)、求b﹣a的平方根;(2)、若在x轴的正半轴上有一点C , 且△ABC的面积是27,求点C的坐标;(3)、过(2)中的点C作直线MN∥y轴,在直线MN上是否存在点D , 使得△ACD的面积是△ABC面积的?若存在,请求出点D的坐标;若不存在,请说明理由.23. 如图,一次函数y1=ax+b的图象与y轴负半轴相交于点A , 与正比例函数y2=kx的图象交于点B(﹣8,6),且 .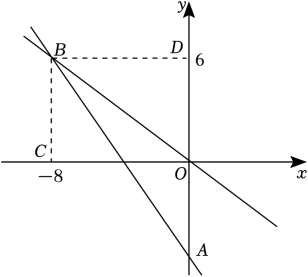 (1)、求正比例函数与一次函数的表达式;(2)、请直接写出当y1>y2时,x的取值范围.24. 通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图1所示的装置测量在不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:
(1)、求正比例函数与一次函数的表达式;(2)、请直接写出当y1>y2时,x的取值范围.24. 通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图1所示的装置测量在不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:砝码的质量m/g
0
50
100
150
200
250
滑动摩擦力f/N
1.8
2.0
2.2
2.4
2.6
2.8
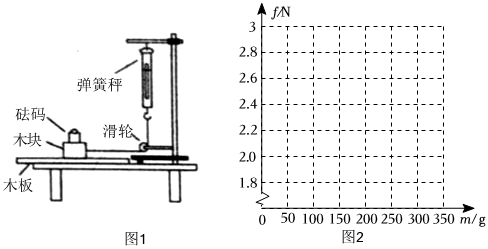 (1)、请在图2的平面直角坐标系内,描出六次测量的有序数对(m , f)所对应的六个点;(2)、这些点是否在一条直线上?如果是,请确定f与m的关系式;如果不是,请说明理由;(3)、在某次实验中,测得木块受到的摩擦力为4.2N , 则此时砝码的质量是多少?(4)、在实验过程中,当砝码的质量为100g~800g时,请直接写出木块受到的摩擦力的最大值和最小值分别为多少?
(1)、请在图2的平面直角坐标系内,描出六次测量的有序数对(m , f)所对应的六个点;(2)、这些点是否在一条直线上?如果是,请确定f与m的关系式;如果不是,请说明理由;(3)、在某次实验中,测得木块受到的摩擦力为4.2N , 则此时砝码的质量是多少?(4)、在实验过程中,当砝码的质量为100g~800g时,请直接写出木块受到的摩擦力的最大值和最小值分别为多少?