安徽省合肥市四十二中2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2024-01-22 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，共40分）

1. 平面直角坐标系中，点 $(a^{2} + 1 ， 2023)$ 所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 若点P是第二象限内的点，且点P到x轴的距离是4，到y轴的距离是5，则点P的坐标是（）

A、（﹣4，5） B、（4，﹣5） C、（﹣5，4） D、（5，﹣4）

查看试题解析
3. 若一个三角形的两边长分别为5和8，则第三边长可能是（）

A、14 B、10 C、3 D、2

查看试题解析
4. 函数y＝ $\frac{\sqrt{x + 2}}{x - 1}$ 中自变量x的取值范围是（　　）

A、x≥﹣2且x≠1 B、x≥﹣2 C、x≠1 D、﹣2≤x＜1

查看试题解析
5. 在平面直角坐标系中，已知函数y＝kx﹣k（k≠0）的图象过点P（2，1），则该函数的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
6. 函数y＝2x﹣1图象向上平移3个单位后，对应函数为（　　）

A、y＝2x+3 B、y＝x﹣5 C、y＝2x+2 D、y＝2x﹣5

查看试题解析
7. 一个三角形三个内角的度数之比是 $2 ： 3 ： 5$ ，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
8. 已知下列命题：①同位角相等；②有一个内角是直角的三角形是直角三角形；③若a＞0，b＞0，则a+b＞0，其中逆命题属于假命题的有（　　）

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 已知直线y＝3x+3﹣a与x轴的交点在A（1，0），B（4，0）之间（包括A ， B两点），则a的取值范围（　　）

A、6＜a＜15 B、1≤a≤4 C、﹣1≤a≤2 D、6≤a≤15

查看试题解析
10. 如图，点 $A$ 、 $B$ 的坐标分别为 $(2 ， 0)$ 、 $(0 ， 1)$ ，点 $P$ 是第一象限内直线 $y = - \frac{1}{2} x + 2$ 上一个动点，当点 $P$ 的横坐标逐渐增大时，四边形 $O A P B$ 的面积（）

A、逐渐增大 B、逐渐减少 C、先减少后增大 D、不变

查看试题解析

二、填空题（本大题共4小题，每小题5分，共20分）

11. 若点P（a+2，1﹣a）在y轴上，则点P的坐标是．

查看试题解析
12. 已知点A（a ， b）在直线y＝﹣3x+5上，则6a+2b﹣10的值为．

查看试题解析
13. 对于一次函数 $y = k x + b$ ，当 $2 \leq x \leq 4$ 时， $3 \leq y \leq 6$ ，则一次函数的解析式为.

查看试题解析
14. 如图，三角形ABC的面积为1，BD：DC＝1：3，E是AC的中点，AD与BE相交于点P ，那么四边形EPDC的面积为．

查看试题解析

三、解答题（本大题共9小题，共90分）

15. 已知平面直角坐标系中有一点M（m﹣1，2m+3）

(1)、当m为何值时，点M到x轴的距离为1？

(2)、当m为何值时，点M到y轴的距离为2？

查看试题解析
16. 已知y是x的一次函数，当x＝2时，y＝3，当x＝﹣2时，y＝﹣5，求：

(1)、这个一次函数的解析式；

(2)、画出该函数的图象．

查看试题解析
17. 如图，在 $△ A B C$ 中， $B D$ 是 $∠ A B C$ 的平分线，且 $∠ A B D = ∠ A$ ， $∠ C = 3 ∠ A$ .

(1)、求 $△ A B C$ 各内角的度数；

(2)、求 $∠ A D B$ 的度数.

查看试题解析
18. 如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为A（﹣5，1），B（﹣4，4），C（﹣1，﹣1）．将△ABC向右平移5个单位长度，再向下平移4个单位长度，得到△A^'B^'C^' ，其中点A^' ， B^' ， C^'分别为点A ， B ， C的对应点．

(1)、请在所给坐标系中画出△A^'B^'C^' ，并直接写出点C^'的坐标；

(2)、若AB边上一点P经过上述平移后的对应点为P^'（x ， y），用含x ， y的式子表示点P的坐标；（直接写出结果即可）

(3)、求△A^'B^'C^'的面积．

查看试题解析
19. 如图，在△ABC中（AC＞AB），AC＝2BC ， BC边上的中线AD把△ABC的周长分成55和45两部分，求AC和AB的长．

查看试题解析
20. 对于平面直角坐标系xOy中的任意一点P（x ， y），给出如下定义：记a＝x+y ， b＝x﹣y ，将点M（a ， b）与N（b ， a）称为点P的一对“相伴点”．例如：点P（2，3）的一对“相伴点”是点（5，﹣1）与（﹣1，5）．

(1)、点Q（4，﹣1）的一对“相伴点”的坐标是与；

(2)、若点A（8，y）的一对“相伴点”重合，则y的值为；

(3)、若点B的一个“相伴点”的坐标为（﹣1，7），求点B的坐标．

查看试题解析
21. 某校八年级学生外出社会实验活动，为了提前做好准备工作，学校安排小车送义工队前往，同时其余学生乘坐客车去目的地，小车到达目的地后立即返回，客车在目的地等候，如图是两车距学校的距离y（千米）与行驶时间x（小时）之间的函数图象．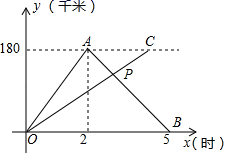

(1)、填空：目的地距离学校千米，小车出发去目的地的行驶速度是千米/时；

(2)、当两车行驶3小时后在途中相遇，求点P的坐标；

(3)、在第（2）题的条件下，求客车到达目的地所用时间．

查看试题解析
22. 已知：在 $△ A B C$ 中， $B O$ 平分 $∠ A B C$ ， $B O$ 、 $C O$ 相交于点 $O$ ，

(1)、如图①，若 $C O ⊥ B C$ ， $∠ B O C = 50 °$ ， $∠ A C B = 42 °$ ，求 $∠ A$ 的大小.

(2)、如图②，若 $C O$ 平分 $∠ A C B$ ，且 $∠ B O C = 3 ∠ A$ ，求 $∠ A$ 的大小.

(3)、如图③，若 $C O$ 在 $△ A B C$ 的外角 $∠ A C M$ 内，且 $∠ A C O ： ∠ O C M = 1 ： 3$ ， $∠ B O C = \frac{4}{5} ∠ A$ ，试探究： $∠ A$ 与 $∠ A B C$ 的数量关系.

查看试题解析
23. 某商场准备购进甲乙两种服装进行销售．甲种服装每件进价160元，售价210元；乙种服装每件进价120元，售价150元．现计划购进两种服装共100件，其中甲种服装不少于60件．设购进甲种服装x件，两种服装全部售完，商场获利y元．

(1)、求y与x之间的函数关系式；

(2)、若购进100件服装的总费用不超过15000元，求最大利润为多少元？

(3)、在（2）的条件下，该服装店对甲种服装以每件优惠a（0＜a＜20）元的价格进行优惠促销活动，乙种服装每件进价减少b元，售价不变，且a﹣b＝4，若最大利润为4000元，求a的值．

查看试题解析