山东省青岛市2023-2024学年七年级上学期期中模考训练试卷
试卷更新日期:2024-01-22 类型:期中考试
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为( )A、 B、 C、 D、2. 一个篮球的单价为a元,一个足球的单价为b元 . 小明买6个篮球和2个足球,小刚买5个篮球和3个足球,则小明比小刚少花( )A、元 B、元 C、元 D、元3. 下列图形经过折叠不能围成棱柱的是( )A、
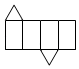 B、
B、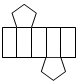 C、
C、 D、
D、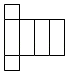 4. 如果单项式与是同类项,那么( )A、1 B、-1 C、 D、5. 已知代数式的值是5,那么代数式的值是( )A、10 B、12 C、16 D、206. 如图1为2018年5月份的日历表,某同学任意框出了其中的四个数字,如图2,若用m表示框图中相应位置的数字,则“?”位置的数字可表示为( )
4. 如果单项式与是同类项,那么( )A、1 B、-1 C、 D、5. 已知代数式的值是5,那么代数式的值是( )A、10 B、12 C、16 D、206. 如图1为2018年5月份的日历表,某同学任意框出了其中的四个数字,如图2,若用m表示框图中相应位置的数字,则“?”位置的数字可表示为( ) A、m+1 B、m+5 C、m+6 D、m+77. 如图所示的运算程序中,若开始输入的x的值为15,则第一次输出的结果为18,
A、m+1 B、m+5 C、m+6 D、m+77. 如图所示的运算程序中,若开始输入的x的值为15,则第一次输出的结果为18,第2次输出的结果为9,...,第2022次输出的结果为( )
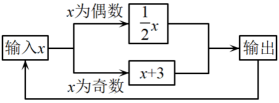 A、3 B、4 C、6 D、98. a是不为2的有理数,我们把称为a的“哈利数”,如3的“哈利数”是 , 的“哈利数”是.已知 , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则( )A、3 B、 C、 D、
A、3 B、4 C、6 D、98. a是不为2的有理数,我们把称为a的“哈利数”,如3的“哈利数”是 , 的“哈利数”是.已知 , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则( )A、3 B、 C、 D、二、填空题(本大题共8小题,每小题3分,共24分)
-
9. 比较大小:﹣ ﹣(填“>”或“<”)10. 如图是一个正方体的表面展开图,已知正方体的每一个面都有一个实数,且相对面上的两个互为倒数,则x的值为.
 11. 我市某天上午的气温为℃,中午上升了3℃,下午下降了2℃,到了夜间又下降了4℃,则夜间的气温为℃.12. A、B为同一数轴上两点,且A、B两点间的距离为3个单位长度,若点A所表示的数是 , 则点B所表示的数是 .13. 已知的值为 , 则代数式的值为 .14. 一个多项式减去x2﹣2y2等于x2+y2 , 则这个多项式是 .15. 互联网支付已经成为北京人民消费的主要支付方式,方便快捷的支付形式也给人们的生活带来了便利.小明妈妈使用某第三方支付平台连续五笔交易情况如图,已知小明妈妈五笔交易前在该支付平台上余额860元,则五笔交易后余额元.
11. 我市某天上午的气温为℃,中午上升了3℃,下午下降了2℃,到了夜间又下降了4℃,则夜间的气温为℃.12. A、B为同一数轴上两点,且A、B两点间的距离为3个单位长度,若点A所表示的数是 , 则点B所表示的数是 .13. 已知的值为 , 则代数式的值为 .14. 一个多项式减去x2﹣2y2等于x2+y2 , 则这个多项式是 .15. 互联网支付已经成为北京人民消费的主要支付方式,方便快捷的支付形式也给人们的生活带来了便利.小明妈妈使用某第三方支付平台连续五笔交易情况如图,已知小明妈妈五笔交易前在该支付平台上余额860元,则五笔交易后余额元.支付宝账单
日期
交易明细
10.16
乘坐公交¥
10.17
转账收入¥
10.18
体育用品¥
10.19
零食¥
10.20
餐费¥
16. 如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第100个图案中的基础图形个数为 .
三、解答题(本大题共7小题,共72分)
-
17. 把下列各数分别在数轴上表示出来,并用“<”连接起来:
, 2, 0, , ,

▲ < ▲ < ▲ < ▲ < ▲ < ▲
18. 计算(1)、(2)、(3)、(4)、19. 如图,是一个由相同的小立方块搭成的几何体从上面看到的平面图,小正方形中的数字表示在该位置的小立方块的个数,请你画出从正面和左面看到的平面图. 20. 某一出租车一天下午以鼓楼为出发点,在东西方向上营运,向东为正,向西为负,行车路程依先后次序记录如下(单位:km):
20. 某一出租车一天下午以鼓楼为出发点,在东西方向上营运,向东为正,向西为负,行车路程依先后次序记录如下(单位:km):+9
-3
-5
+4
-8
+6
-3
-6
-4
+7
(1)、将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼什么方向?(2)、将最后一名乘客送到目的地,出租车一共行驶多少千米?(3)、若每千米的价格为2.4元,司机一下午的营运额是多少元?21.(1)、已知 , , 求;(2)、先化简,再求值: , 其中 .22. 某餐厅中,一张桌子可坐6人,有以下两种摆放方式: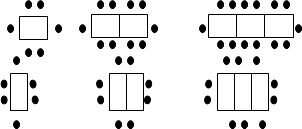 (1)、当有n张桌子时,两种摆放方式各能坐多少人?
(1)、当有n张桌子时,两种摆放方式各能坐多少人?
(2)、一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
23. 【问题提出】在学习数轴知识时,数学小组的同学们遇到了这样的问题,请你帮他们解决:若将数轴折叠,使与4表示的点重合.(1)、则表示的点与数表示的点重合;(2)、若数轴上M、N两点之间的距离为2022,且M、N两点经过上述方法折叠后互相重合,求M , N两点表示的数.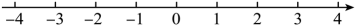 (3)、【反思生疑】解决这个问题后,小寻同学提出了这样的问题:既然数轴可以折叠,那可不可以把数轴旋转一下呢?于是,同学们将数轴绕原点旋转 , 得到了如图的“新数轴”:
(3)、【反思生疑】解决这个问题后,小寻同学提出了这样的问题:既然数轴可以折叠,那可不可以把数轴旋转一下呢?于是,同学们将数轴绕原点旋转 , 得到了如图的“新数轴”: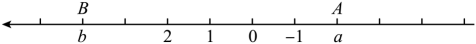
晓晓同学说:一般规定向右为数轴的正方向,但是如果规定“向左”为正方向,也可以帮助我们解决问题.我们就叫这个数轴为“新数轴”吧!我来考考大家:
在这个“新数轴”上, , , 点A与点B之间的距离为;
(4)、在这个“新数轴”上,若点P从A出发,以每秒2个单位长度的速度向左移动,经过多少秒,点P与点A的距离是点P与点B的距离的2倍?此时,点P在“新数轴”上对应的数是多少?