安徽省合肥市蜀山区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-22 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 点在平面直角坐标系中的第( )象限.A、一 B、二 C、三 D、四2. 已知点在轴上,位于原点左侧,到原点的距离为3个单位长度,则点的坐标是( )A、 B、 C、 D、3. 在圆周长的计算公式中,变量有( )A、 , B、 , C、 , D、 ,4. 函数①;②;③;④;⑤ , 是一次函数的有( )A、1个 B、2个 C、3个 D、4个5. 将直线向右平移2个单位后所得图象对应的函数表达式为( )A、 B、 C、 D、6. 晚饭后彤彤和妈妈散步到小区旁边的公园,在公园中央的休息区昴了会天,然后一起跑步回家,下面能反映彤彤和妈妈离家的距离与时间的函数关系的大致图象是( )A、
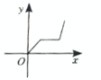 B、
B、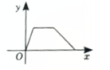 C、
C、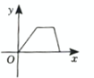 D、
D、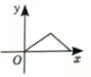 7. 将三角尺和直尺如图所示叠放在一起,已知 , 则( )
7. 将三角尺和直尺如图所示叠放在一起,已知 , 则( ) A、 B、 C、 D、8. 如图,在中,是中点,是中点,连接、 , 若与的面积差为6,则的面积为( )
A、 B、 C、 D、8. 如图,在中,是中点,是中点,连接、 , 若与的面积差为6,则的面积为( )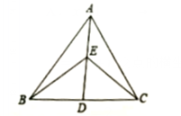 A、9 B、12 C、15 D、189. 如图,直线与轴交点的横坐标为1,则关于的方程的解为( )
A、9 B、12 C、15 D、189. 如图,直线与轴交点的横坐标为1,则关于的方程的解为( )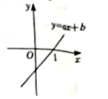 A、 B、 C、 D、10. 如图,直线与交点的横坐标为1,若与轴的所夹儌角为 , 则方程组解为( )
A、 B、 C、 D、10. 如图,直线与交点的横坐标为1,若与轴的所夹儌角为 , 则方程组解为( )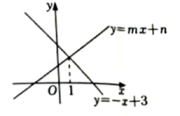 A、 B、 C、 D、无解
A、 B、 C、 D、无解二、填空题(每小题5分,共20分)
-
11. 已知点 , 则点到轴的距离是.12. 函数中,自变量的取值范围是.13. 当时,一次函数的最小值为 , 则.14. 如图:点 , 分别是的、边上的点,将纸片沿折叠使点落在点处,①若 , , 则的度数为.
②若 , 始终保持在 , 边上时(不和点重合), , , 且为锐角,当点落在内部时,则.(用含有 , 的代数式表示)

三、解答题(每小题8分,共32分)
-
15. 在平面直角坐标系中,线段的两端点的坐标分别为 , , 将线段向下平移2个单位,再向右平移4个单位得线段(与对应,与对应).
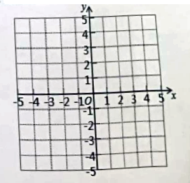 (1)、画出线段与线段;并写出点、点的坐标.(2)、求四边形的面积.16. 已知是关于的一次函数,点 , 在函数图象上.(1)、求该函数的解析式;(2)、当时,求的值.17. 如图,是的边上一点, , , .求:
(1)、画出线段与线段;并写出点、点的坐标.(2)、求四边形的面积.16. 已知是关于的一次函数,点 , 在函数图象上.(1)、求该函数的解析式;(2)、当时,求的值.17. 如图,是的边上一点, , , .求: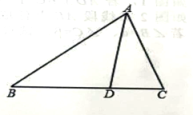 (1)、的度数;(2)、的度数.18. 某乡镇企业现在年产值是15万元,如果每增加5万元投资,一年增加10万元产值,求出总产值(万元)与新增加的投资额万元之间函数关系.
(1)、的度数;(2)、的度数.18. 某乡镇企业现在年产值是15万元,如果每增加5万元投资,一年增加10万元产值,求出总产值(万元)与新增加的投资额万元之间函数关系.四、解答题(每小题10分,共20分)
-
19. 已如三角形的三条边长为3、5和.(1)、若3是该三角形的最短边长,求的取值范围;(2)、若为整数,求三角形周长的最大值.20. 在中,平分 , .
图1
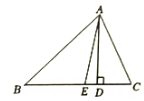 图2
图2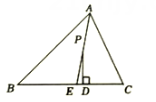 (1)、如图1,若于点 , , , 求的度数.(2)、如图2在线段上任取一点(不与 , 重合),过点作于点 , 若 , .试求出的度数.(用含有、的代数式表示即可)
(1)、如图1,若于点 , , , 求的度数.(2)、如图2在线段上任取一点(不与 , 重合),过点作于点 , 若 , .试求出的度数.(用含有、的代数式表示即可)五、解答题(每小题12分,共24分)
-
21. 如图,已知函数和的图象交于点 , 这两个函数的图象与轴分别交于点、.
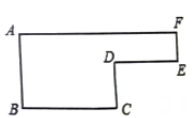
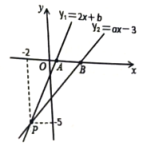 (1)、分别求出这两个函数的解析式;(2)、求的面积;(3)、根据图象直接写出不等式的解集.22. 如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点以每秒的速度沿图甲的边框按从的路径移动,相应的的面积与时间之间的关系如图乙中的图象表示.若 , 试回答下列问题:
(1)、分别求出这两个函数的解析式;(2)、求的面积;(3)、根据图象直接写出不等式的解集.22. 如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点以每秒的速度沿图甲的边框按从的路径移动,相应的的面积与时间之间的关系如图乙中的图象表示.若 , 试回答下列问题:图甲
 图乙
图乙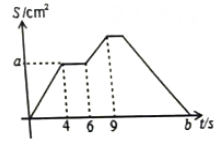 (1)、填空:图甲中的 , ;(2)、求:图乙中的的值;(3)、求:图乙中的的值.
(1)、填空:图甲中的 , ;(2)、求:图乙中的的值;(3)、求:图乙中的的值.六、解答题(14分)
-
23. 在平面直角坐标系中,点为坐标原点,直线交轴于点 , 交轴于点 , 且.
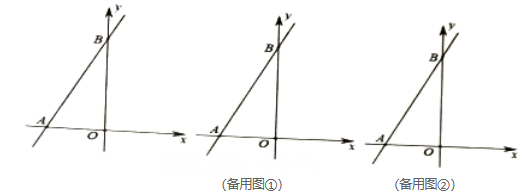 (1)、求直线的解析式;(2)、①若另一条直线与直线有唯一交点 , 求点的坐标;
(1)、求直线的解析式;(2)、①若另一条直线与直线有唯一交点 , 求点的坐标;②直接写出的取值范围.
(3)、若直线只与轴的交点在线段上(不与 , 重合),试写出取值范围.