四川省泸州市叙永县一中教育共同体第一次大联考2023-2024学年七年级上学期12月月考数学试题

试卷更新日期：2024-01-22 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12个小题，每小题3分，满分36分）

1. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入150元记作 $+ 150$ ，那么 $- 90$ 元表示（）

A、收入10元 B、支出90元 C、收入90元 D、支出10元

查看试题解析
2. 下列各组数中，互为倒数的是（）

A、3与 $- 3$ B、3与 $- \frac{1}{3}$ C、 $- 3$ 与 $\frac{1}{3}$ D、 $- 3$ 与 $- \frac{1}{3}$

查看试题解析
3. 单项式 $- 3 x y^{2}$ 系数与次数分别是（）

A、3与2 B、 $- 3$ 与2 C、 $- 3$ 与3 D、3与3

查看试题解析
4. 方程 $2 x = - \frac{1}{2}$ 的解是（）

A、 $x = - \frac{1}{4}$ B、 $x = - 1$ C、 $x = \frac{1}{4}$ D、 $x = 1$

查看试题解析
5. 神舟十号飞船是我国“神舟”系列飞船之一，每小时飞行约 $28000000$ 米，将 $28000000$ 用科学记数法表示为（）

A、 $2.8 \times 1 0^{8}$ B、 $28 \times 1 0^{6}$ C、 $2.8 \times 1 0^{7}$ D、 $0.28 \times 1 0^{8}$

查看试题解析
6. 已知等式 $6 a = 9 b + 8$ ，则下列等式中不一定成立的是（）

A、 $6 a - 8 = 9 b$ B、 $6 a + 3 = 9 b + 11$ C、 $a = \frac{3}{2} b + \frac{4}{3}$ D、 $6 a c = 9 b c + 8$

查看试题解析
7. 多项式8x²﹣3x+5与3x³﹣4mx²﹣5x+7多项式相加后，不含二次项，则m的值是（）

A、2 B、4 C、﹣2 D、﹣4

查看试题解析
8. 粉刷一个房间甲单独做4天完成，乙单独做6天完成，丙单独做12天完成．甲先单独做2天后有事离开，接下来乙、丙共同完成，则乙、丙合作所需要的天数为（）

A、1 B、2 C、3 D、4

查看试题解析
9. $a 、 b$ 是有理数，它们在数轴上的对应点的位置如图所示，把 $a$ 、 $- a$ 、 $b$ 、 $- b$ 按照从小到大的顺序排列是（）

A、 $- b < - a < a < b$ B、 $- a < - b < a < b$ C、 $- b < a < - a < b$ D、 $- b < b < - a < a$

查看试题解析
10. 一辆货轮往返于上下两个码头，逆流而上需用38小时，顺流而下需用32小时，若水流速度为8千米/时，则下列求两码头距离 $x$ 的方程正确的是（）

A、 $\frac{x}{32} - 8 = \frac{x}{38} + 8$ . B、 $\frac{x - 8}{36} = \frac{x + 8}{38}$ C、 $\frac{x}{32} - \frac{x}{38} = \frac{8}{2}$ D、 $\frac{2 x}{32 + 38} = \frac{1}{2} (\frac{x}{32} + \frac{x}{38})$

查看试题解析
11. 已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形，小明把这2个小长方形按如图所示放置在大长方形中，小明经过推事得知，要求出图中阴影部分的周长之和，只需知道a、b、m、n中的一个量即可，则要知道的那个量是（）

A、a B、b C、m D、n

查看试题解析
12. 观察下面一列数： $- 1 ， 2 ， - 3 ， 4 ， - 5 ， 6 ， - 7 ⋯$ 将这列数排成下列形式：
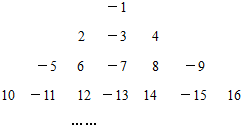
照上述规律排下去，则第九行中左边第6个数是（）

A、70 B、 $- 70$ C、69 D、 $- 69$

查看试题解析

二、填空题（本大题共4个小题，每小题3分，满分12分）

13. 用四舍五入法将 $2.173$ 精确到百分位为．

查看试题解析
14. 如果代数式 $2 a + b + 1$ 的值是3，则 $6 a + 3 b - 1$ 的值是．

查看试题解析
15. 足球比赛的记分为：胜一场得3分，平一场得1分，负一场得0分，一队打了14场比赛，负5场，共得21分，那么这个队胜了场．

查看试题解析
16. 某商场购进一批服装，又恰巧碰到双十一的促销活动，商场决定将这批服装按标价的五折销售，若打折后每件服装可获利润60元，其利润率为 $10 %$ ；若双十一过后，该商场按这批服装的标价打八折出售，那么获得的利润是元．

查看试题解析

三、计算题（本大题共3个小题，每小题6分，满分18分）

17. 计算： $18 + 32 \div {(- 2)}^{3} - {(- 4)}^{2} \times 5$

查看试题解析
18. 计算： $- 1^{2014} + [2 - (- 3^{2})] - \frac{1}{4} - | \frac{5}{4} - 2 |$

查看试题解析
19. 解方程： $\frac{3 x - 1}{4} = 1 - \frac{x + 8}{6}$

查看试题解析

四、解答题（本大题共2个小题，每小题7分，满分14分）

20. 已知下列各有理数： $- 2.5$ ，0， $| - 3 |$ ， $- (- 2)$ ， $\frac{1}{2}$ ， $- 1 \dots$

(1)、画出数轴，在数轴上标出这些数表示的点；

(2)、用“ $<$ ”号把这些数连接起来.

查看试题解析
21. 先化简,再求值： $2 (3 x y^{2} - 2 x^{2} y) - 3 (2 x y^{2} - x^{2} y) + 4 (x y^{2} - 2 x^{2} y)$ ,其中 $x = - 2$ , $y = - 1$ ．

查看试题解析

五、解答题（本大题共2个小题，每小题8分，满分16分）

22. 下表是2023年12月的日历，用如图所示的L形框去框其中的4个数．
2023年12月

(1)、设被框住的最小的数为x ，用含x的代数式表示出被框住的这4个数的和为；

(2)、被框住的4个数的和能等于100吗？如果能，求出这4个数；如果不能，说明理由．

查看试题解析
23. 观察下列等式 $\frac{1}{1 \times 2} = 1 - \frac{1}{2} ， \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ， \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，将以上三个等式两边分别相加得： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ ．

(1)、猜想并写出： $\frac{1}{n (n + 1)}$ ▲ ；

(2)、解方程： $\frac{x}{1 \times 2} + \frac{x}{2 \times 3} + \frac{x}{3 \times 4} + ⋯ + \frac{x}{2022 \times 2023} = 2022$ ．

查看试题解析

六、解答题（本大题共2个小题，每小题12分，满分24分）

24. 点 $A$ 、 $B$ 、 $C$ 在数轴上表示的数是 $a$ ， $b$ ， $c$ ，且满足 ${(a + 7)}^{2} + | b - 5 | = 0$ ，多项式 $x^{| c + 3 |} y^{3} - (c + 5) x^{3} + x y^{2} - 1$ 是五次四项式．

(1)、 $a$ 的值为 ▲ ， $b$ 的值为 ▲ ， $c$ 的值为 ▲ ．

(2)、若点 $A$ 以每秒2个单位的速度向左运动，同时点 $B$ 、 $C$ 分别以每秒4个单位、1个单位的速度向右移动，设移动时间为 $t$ 秒．
①点 $C$ 表示的数是 ▲ （用含有 $t$ 的代数式表示）；
②当 $t = 5$ 秒时，求 $A C - C B$ 的值；
③试探索： $A C - C B$ 的值是否随着时间 $t$ 的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析
25. 某地今年夏季降雨量大幅下降，水电发电量严重受限，再加上高温天气持续，居民用电量居高不下，电力供需形势十分严峻．已知该地为节约用电，利用价格调控的手段，规定了居民生活用电的阶梯收费标准如表：
价目表
每月用电量
价格
不超过180千瓦时的部分
$0.52$ 元 $/$ 千瓦时
超过180千瓦时，但不超过280千瓦时的部分
$0.62$ 元 $/$ 千瓦时
超过280千瓦时的部分
$0.82$ 元 $/$ 千瓦时

(1)、若小明家8月份用电200千瓦时，则应缴多少电费；

(2)、若小明家8月份用电 $a$ 千瓦时（其中 $a > 280$ ），则应缴多少电费；（用含 $a$ 的代数式表示，并化简）

(3)、若小明家8月份缴电费336元，求小明家8月份用电多少千瓦时．

查看试题解析

价目表
每月用电量	价格
不超过180千瓦时的部分	$0.52$ 元 $/$ 千瓦时
超过180千瓦时，但不超过280千瓦时的部分	$0.62$ 元 $/$ 千瓦时
超过280千瓦时的部分	$0.82$ 元 $/$ 千瓦时