吉林省吉林市磐石市2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-01-22 类型:期末考试
一、单项选择题(每小题2分,共12分)
-
1. 一元二次方程配方后可化为( )A、 B、 C、 D、2. 某物体的三视图如图所示,那么该物体的形状是( )
 A、三棱柱 B、长方体 C、正方体 D、圆锥3. 如图,已知∠ACB是⊙O的圆周角,∠ACB=50°,则圆心角∠AOB是( )
A、三棱柱 B、长方体 C、正方体 D、圆锥3. 如图,已知∠ACB是⊙O的圆周角,∠ACB=50°,则圆心角∠AOB是( ) A、40° B、50° C、80° D、100°4. 如图,DE是的中位线,M是DE的中点,CM的延长线交AB于点N , 则等于( )
A、40° B、50° C、80° D、100°4. 如图,DE是的中位线,M是DE的中点,CM的延长线交AB于点N , 则等于( ) A、1∶2 B、1∶3 C、1∶4 D、1∶55. ⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( )
A、1∶2 B、1∶3 C、1∶4 D、1∶55. ⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( )
A、相离 B、相切 C、相交 D、内含6. 如图,下列结论中错误的是( ) A、方程的解为 , B、当时,有 C、 , , D、直线与两坐标轴围成的三角形的面积是
A、方程的解为 , B、当时,有 C、 , , D、直线与两坐标轴围成的三角形的面积是二、填空题(每小题3分,共24分)
-
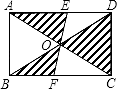
7. 若1000张奖券中有200张可以中奖,则从中任抽1张能中奖的概率为.8. 同一圆中,一条弧所对的圆心角和圆周角分别为和90°,则.9. 已知圆锥的底面半径为3cm,母线长为4cm,则该圆锥侧面展开图的面积为 cm2.10. 若有一个因式是 , 则k的值是.11. 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
 12. 用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系 , 则该矩形面积的最大值为 m2.13. 如图所示,在中, , , , 则AB的长为.
12. 用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系 , 则该矩形面积的最大值为 m2.13. 如图所示,在中, , , , 则AB的长为. 14. 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2020次,点P依次落在点P1 , P2 , P3 , P4 , …,P2020的位置,则P2020的横坐标x2020=
14. 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2020次,点P依次落在点P1 , P2 , P3 , P4 , …,P2020的位置,则P2020的横坐标x2020=
三、解答题(每小题5分,共20分)
-
15. 为进一步促进义务教育均衡发展,某县加大了基础教育经费的投入,已知2018年该县投入基础教育经费5000万元,2020年投入基础教育经费7200万元,求该县这两年投入基础教育经费的年平均增长率.16. 已知一次函数平行于直线 , 且与双曲线的一个交点为 , 求此一次此函数的解析式.17. 如图,在中,AD是的平分线,过点C的射线CE交AD的延长线于E , 且 , 求证:.
 18. 如图,内接于 , , , BD为直径, , 求弦DC的长.
18. 如图,内接于 , , , BD为直径, , 求弦DC的长.
四、解答题(每小题7分,共28分)
-
19. 某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.(1)、求甲、乙、丙三名学生在同一个餐厅用餐的概率;(2)、求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率.20. 如图,正方形MNPQ的顶点在三角形ABC的边上,当边BC的长a与高AD的长h满足什么条件时,正方形MNPQ的面积是三角形ABC面积的一半?
 21. 已知二次函数的图象过原点,与x轴交于点.(1)、求这个二次函数的表达式;(2)、在抛物线上存在点P , 满足 , 请直接写出点P的坐标.22. 青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃. 如图,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°,已知米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位,)
21. 已知二次函数的图象过原点,与x轴交于点.(1)、求这个二次函数的表达式;(2)、在抛物线上存在点P , 满足 , 请直接写出点P的坐标.22. 青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃. 如图,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°,已知米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位,)
五、解答题(每小题8分,共16分)
-
23. 如图,AB是的直径,AD与相切于点A , 过B点作交于点C , 连接OC、AC , AC交OD于点E.
 (1)、求证:;(2)、若 , , 求图中阴影部分的面积.(结果保留)24. 如图,已知反比例函数和一次函数交于点A , 其中一次函数的图象经过、两点.
(1)、求证:;(2)、若 , , 求图中阴影部分的面积.(结果保留)24. 如图,已知反比例函数和一次函数交于点A , 其中一次函数的图象经过、两点. (1)、求反比例函数的解析式;(2)、若点A的坐标为(1,1),在x轴上是否存在点P , 使为等腰三角形?
(1)、求反比例函数的解析式;(2)、若点A的坐标为(1,1),在x轴上是否存在点P , 使为等腰三角形?六、解答题(每小题10分,共20分)
-
25. 在中,D为AB边上一点,过点D作交AC于点E , 以DE为折线,将翻折,设所得的与梯形DBCE重叠部分的面积为y.
图1
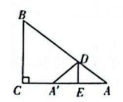 图2
图2  图3
图3 (1)、如图1,若 , , , , 则y的值为;(2)、如图2,若 , , D为AB中点,则y的值为;(3)、若 , , , 设.
(1)、如图1,若 , , , , 则y的值为;(2)、如图2,若 , , D为AB中点,则y的值为;(3)、若 , , , 设.①求y与x的函数解析式;
②y是否有最大值,若有,求出y的最大值;若没有,请说明理由.
26. 如图,抛物线与双曲线相交于点A、B.已知点B的坐标为 , 点A在第一象限内,且点A的横坐标为1.过点A作直线轴,交抛物线于另一点C. (1)、求双曲线和抛物线的解析式;(2)、计算的面积;(3)、在抛物线上是否存在点D , 使的面积等于的面积,若存在,请你写出点D的坐标;若不存在,请你说明理由.
(1)、求双曲线和抛物线的解析式;(2)、计算的面积;(3)、在抛物线上是否存在点D , 使的面积等于的面积,若存在,请你写出点D的坐标;若不存在,请你说明理由.