吉林省长春市九台区2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-01-22 类型:期末考试
一、选择题(本大题共8道题,每题3分,共24分)
-
1. 8的立方根是( )A、2 B、 C、4 D、2. 计算 的结果是( )A、 B、 C、 D、3. 面积为的长方形一边长为另一边长为( )A、 B、 C、 D、4. 直角三角形的两边长分别为a,b,且a,b满足 +|b﹣4|=0,则此三角形的第三长为( )A、5 B、25 C、 D、5或5. 下面四幅图中,不能证明勾股定理的是( )A、
 B、
B、 C、
C、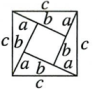 D、
D、 6. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 , 提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
6. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 , 提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( ) A、 B、 C、 D、7. 在中,根据下列尺规作图的痕迹,不能判断与大小关系的是( )A、
A、 B、 C、 D、7. 在中,根据下列尺规作图的痕迹,不能判断与大小关系的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,中, , 将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ).
8. 如图,中, , 将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ). A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题(本大题共6道题,每题3分,共18分)
-
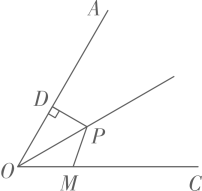
9. 若 , 则的值为 .10. 已知△ABC是等腰三角形.若∠A=40°,则△ABC的顶角度数是 .11. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .
 12. 如图,在数轴上点 A 表示的实数是 .
12. 如图,在数轴上点 A 表示的实数是 . 13. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=cm.
13. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=cm. 14. 如图,已知圆柱底面的周长为6dm,圆柱高为4dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
14. 如图,已知圆柱底面的周长为6dm,圆柱高为4dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
三、解答题(本大题共78分)
-
15. 先化简,再求值: , 其中16. 已知 , ,求 的值.17. 图①、图②、图③都是的正方形网格,每个小正方形的顶点称为格点.均在格点上,按下列要求画图:
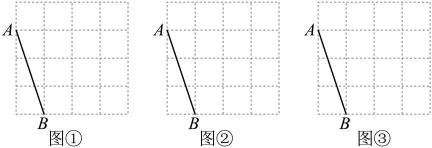 (1)、在图①中,以格点为顶点,画以为底边的等腰;(2)、在图②中,以格点为顶点,画出以为腰的等腰;(3)、在图③中,以格点为顶点,画出以为腰的等腰 , 并且所画的与图②中所画的不全等.18. 阅读下列材料:
(1)、在图①中,以格点为顶点,画以为底边的等腰;(2)、在图②中,以格点为顶点,画出以为腰的等腰;(3)、在图③中,以格点为顶点,画出以为腰的等腰 , 并且所画的与图②中所画的不全等.18. 阅读下列材料:一般地,没有公因式的多项式,当项数为四项或四项以上时,经常把这些项分成若干组,然后各组运用提取公因式法或公式法分别进行分解,之后各组之间再运用提取公因式法或公式法进行分解,这种因式分解的方法叫做分组分解法.如:
因式分解:am+bm+an+bn
=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n).
(1)、利用分组分解法分解因式:①3m﹣3y+am﹣ay;
②a2x+a2y+b2x+b2y .
(2)、因式分解:a2+2ab+b2﹣1=(直接写出结果).19. 小聪、小明参加了100米跑的5期集训,每期集训结束时进行测试.根据他们集训时间、测试成绩绘制成如下两个统计图.
根据图中信息,解答下列问题:
(1)、这5期的集训共有多少天?(2)、小明参加集训第期时成绩最好,此期集训的天数是天,最好成绩为秒;(3)、哪一期小聪的成绩比他上一期的成绩进步最多?进步了多少秒?20. 如图,点E在△ABC外部,点D在边BC上,DE交AC于点F , 若 , . (1)、求证:;(2)、若 , , 求∠E的度数.21. 党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许多城市再现绿水青山.某小区物业在小区拐角清理出了一块空地进行绿化改造,如图, , .
(1)、求证:;(2)、若 , , 求∠E的度数.21. 党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许多城市再现绿水青山.某小区物业在小区拐角清理出了一块空地进行绿化改造,如图, , .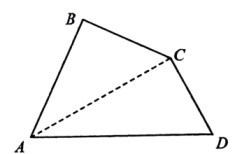 (1)、为了方便居民的生活,在绿化时将修一条从点直通点的小路,求小路的长度;(2)、若该空地的改造费用为每平方米150元,试计算改造这片空地共需花费多少元?22.(1)、如图1,已知:在中, , 平分 , 平分 , 过点D作 , 分别交、于、两点,则图中共有个等腰三角形;与、之间的数量关系是 , 的周长是 .
(1)、为了方便居民的生活,在绿化时将修一条从点直通点的小路,求小路的长度;(2)、若该空地的改造费用为每平方米150元,试计算改造这片空地共需花费多少元?22.(1)、如图1,已知:在中, , 平分 , 平分 , 过点D作 , 分别交、于、两点,则图中共有个等腰三角形;与、之间的数量关系是 , 的周长是 .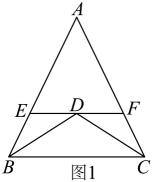 (2)、如图2,若将(1)中“中,”改为“”其余条件不变,则与、之间的数量关系?证明你的结论.
(2)、如图2,若将(1)中“中,”改为“”其余条件不变,则与、之间的数量关系?证明你的结论.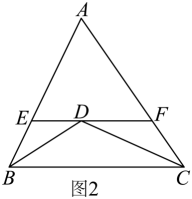 (3)、已知:如图3,在外, , 且平分 , 平分的外角 , 过点作分别交、于、两点,则与、之间又有何数量关系 .
(3)、已知:如图3,在外, , 且平分 , 平分的外角 , 过点作分别交、于、两点,则与、之间又有何数量关系 . 23. 阅读下列材料:
23. 阅读下列材料:我们把形如及的式子叫做完全平方式,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.
例如:把二次三项式进行配方.
(1)、【直接应用】把二次三项式配方;(2)、代数式的最小值为;(3)、【类比应用】已知(为任意实数),则与的大小关系是(填“”、“”或“”)(4)、当分别为的三边,且满足 , 判断此时的形状并说明理由.24. 如图,中, , 点M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,点M个速度为 , 点N的速度为 , 当点M、N第一次相遇时,点M、N同时停止运动,设点M、N的运动时间为秒.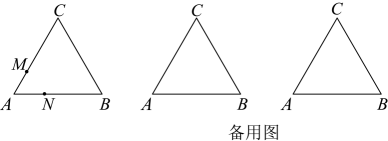 (1)、当点M在上时,;当点M在上时,(用含t的代数式表示).(2)、点N在上时,若为直角三角形,求t的值.(3)、连结 , 当的对称轴垂直平分线段时,直接写出t的值.
(1)、当点M在上时,;当点M在上时,(用含t的代数式表示).(2)、点N在上时,若为直角三角形,求t的值.(3)、连结 , 当的对称轴垂直平分线段时,直接写出t的值.