贵州省毕节市2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-01-22 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 在实数 , , , , , 每两个之间依次多个中,无理数的个数是( )A、个 B、个 C、个 D、个2. 一组数据2,2,4,3,6,5,2的众数和中位数分别是A、3,2 B、2,3 C、2,2 D、2,43. 若点关于原点的对称点是 , 则的值是( )A、 B、 C、 D、4. 下列语句不正确的是( )A、数轴上表示的数,如果不是有理数,那么一定是无理数
B、大小介于两个有理数之间的无理数有无数个
C、的立方是 , 立方根也是 D、两个实数,较大者的平方也较大5. 如图,已知 , , , 则的度数为( ) A、 B、 C、 D、6. 在年月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有名学生参加决赛.他们决赛的成绩各不相同,其中的一名学生想要知道自己能否进入前名,不仅要了解自己的成绩,还要了解这名学生成绩的( )A、众数 B、中位数 C、平均数 D、方差7. 在 , , 这些实数中,无理数有个( ).A、 B、 C、 D、8. 下列运算正确的是( )A、 B、 C、 D、9. 下列能用平方差公式计算的是( )A、 B、 C、 D、10. 已知x2+16x+k是完全平方式,则常数k等于( )A、64 B、48 C、32 D、1611. 计算的结果是( )A、 B、 C、 D、12. 如图,在中,与的平分线交于点 , 过点作 , 分别交、于点、若 , , 则的周长为( )
A、 B、 C、 D、6. 在年月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有名学生参加决赛.他们决赛的成绩各不相同,其中的一名学生想要知道自己能否进入前名,不仅要了解自己的成绩,还要了解这名学生成绩的( )A、众数 B、中位数 C、平均数 D、方差7. 在 , , 这些实数中,无理数有个( ).A、 B、 C、 D、8. 下列运算正确的是( )A、 B、 C、 D、9. 下列能用平方差公式计算的是( )A、 B、 C、 D、10. 已知x2+16x+k是完全平方式,则常数k等于( )A、64 B、48 C、32 D、1611. 计算的结果是( )A、 B、 C、 D、12. 如图,在中,与的平分线交于点 , 过点作 , 分别交、于点、若 , , 则的周长为( )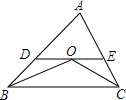 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共5小题,每小题3分,共15分。
-
13. 的立方根是 .14. 要使分式的值为零,和的取值应为 .15. 想让关于的分式方程没有增根,则的值为 填一个 .16. 如图,将长为的弹性绳放置在直线上,固定端点和 , 然后把中点竖直向上拉升至点 , 则拉长后弹性绳的长为 .
 17. 已知一张三角形纸片如图甲 , 其中 , 将纸片沿过点的直线折叠,使点落到边上的点处,折痕为如图乙 , 再将纸片沿过点的直线折叠,点恰好与点重合,折痕为如图丙原三角形纸片中,的大小为 .
17. 已知一张三角形纸片如图甲 , 其中 , 将纸片沿过点的直线折叠,使点落到边上的点处,折痕为如图乙 , 再将纸片沿过点的直线折叠,点恰好与点重合,折痕为如图丙原三角形纸片中,的大小为 .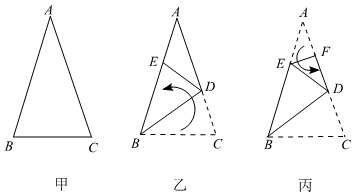
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
-
18. 在计算时,小明的解题过程如下:
解:原式
(1)、老师认为小明的解法有错,请你指出小明从第步开始出错的;(2)、请你给出正确的解题过程.19. 老师在黑板上书写了一个代数式的正确计算结果,随后用手遮住了原代数式的一部分,如图: .(1)、求被手遮住部分的代数式,并将其化简;
(2)、原代数式的值能等于吗?请说明理由.20. 已知,如图,是的边上一点,交于点 , , ,
求证: .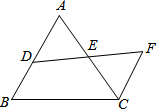 21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).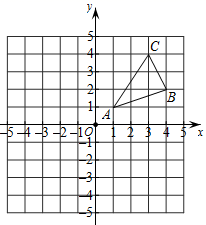 (1)、请画出△ABC关于x轴成轴对称的图形△A1B1C1 , 并写出A1、B1、C1的坐标;(2)、在y轴上找一点P,使PA+PB的值最小,请画出点P的位置.22. 我国的动车和高铁技术处于全球领先位置,是“中国制造”的闪亮名片,高铁和普通列车的双普及模式,极大方便了人民群众出行.上世纪60年代通车的京广铁路广州一长沙段全程1000公里,而广州至长沙的高铁里程是普通列车铁路里程的 .(1)、广州至长沙的高铁里程是公里;(2)、若广州至长沙的高铁平均速度(公里/小时)是普通列车平均速度(公里/小时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少7个小时,求高铁的平均速度.23. 如图,和都是正三角形,和交于点 .
(1)、请画出△ABC关于x轴成轴对称的图形△A1B1C1 , 并写出A1、B1、C1的坐标;(2)、在y轴上找一点P,使PA+PB的值最小,请画出点P的位置.22. 我国的动车和高铁技术处于全球领先位置,是“中国制造”的闪亮名片,高铁和普通列车的双普及模式,极大方便了人民群众出行.上世纪60年代通车的京广铁路广州一长沙段全程1000公里,而广州至长沙的高铁里程是普通列车铁路里程的 .(1)、广州至长沙的高铁里程是公里;(2)、若广州至长沙的高铁平均速度(公里/小时)是普通列车平均速度(公里/小时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少7个小时,求高铁的平均速度.23. 如图,和都是正三角形,和交于点 .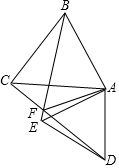 (1)、求证:≌;
(1)、求证:≌;
(2)、求证:平分 .