贵州省毕节市重点中学2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-01-22 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )A、+0.25m B、-0.25m C、+0.35m D、-0.35m2. 下边的立体图形是由哪个平面图形绕轴旋转一周得到的( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在有理数 , , 中,负数的个数有( )A、个 B、个 C、个 D、个4. 下列合并同类项的结果中,正确的是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、的系数是 B、的常数项是 C、次数是次 D、是二次多项式6. 下列说法正确的是( )A、的底数是 B、表示个相加 C、与意义相同 D、的底数是7. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式8. 如果 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或9. 下列各式中是一元一次方程的是( )A、 B、 C、 D、10. 下列变形正确的是( )A、变形得 B、变形得 C、变形得 D、变形得11. 如图, , 点 , , 在同一直线上,若 , 则的度数为( )
3. 在有理数 , , 中,负数的个数有( )A、个 B、个 C、个 D、个4. 下列合并同类项的结果中,正确的是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、的系数是 B、的常数项是 C、次数是次 D、是二次多项式6. 下列说法正确的是( )A、的底数是 B、表示个相加 C、与意义相同 D、的底数是7. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式8. 如果 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或9. 下列各式中是一元一次方程的是( )A、 B、 C、 D、10. 下列变形正确的是( )A、变形得 B、变形得 C、变形得 D、变形得11. 如图, , 点 , , 在同一直线上,若 , 则的度数为( )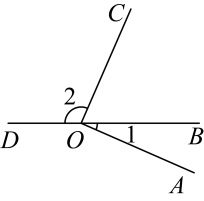 A、113° B、 C、 D、12. 如图图形都是由同样大小的小圆圈按一定规律组成的,其中第个图形中共有个小圆圈,第个图形中共有个小圆圈,第个图形中共有个小圆圈, , 按此规律,则第个图形中小圆圈的个数为( )
A、113° B、 C、 D、12. 如图图形都是由同样大小的小圆圈按一定规律组成的,其中第个图形中共有个小圆圈,第个图形中共有个小圆圈,第个图形中共有个小圆圈, , 按此规律,则第个图形中小圆圈的个数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共4小题,每小题4分,共16分。
-
13. 的相反数是 ,绝对值是 ,倒数是 .14. 已知与是同类项,则 .15. 如图,以为圆心的扇形与扇形的圆心角为 , 若 , , 则阴影部分的面积为 .
 16. 如图是一个正方体的平面展开图,若将其按虚线折叠成正方体后,相对面上的两个数字之和均为 , 则 .
16. 如图是一个正方体的平面展开图,若将其按虚线折叠成正方体后,相对面上的两个数字之和均为 , 则 .
三、解答题:本题共9小题,共98分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:
(1)、;
(2)、 .18. 解方程:
(1)、;
(2)、 .19. 先化简,再求值: , 其中 , .20. 已知 , , 请按要求解决以下问题:(1)、求;
(2)、若的值与的取值无关,求的值.21. 如图,线段 , 是线段上一点, , 、分别是、的中点.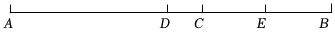 (1)、求线段的长;
(1)、求线段的长;
(2)、求线段的长.22. 某学校拟举办“双减”背景下的初中数学活动型作业成果展示现场会,为了解学生最喜爱的项目,现随机抽取若干名学生进行调查,并将调查结果绘制成如图两幅不完整的统计图: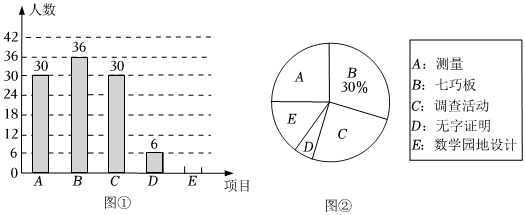
根据以上信息,解答下列问题:(1)、参与此次抽样调查的学生人数是 人,补全统计图要求在条形图上方注明人数;(2)、图中扇形的圆心角度数为 度;(3)、若参加成果展示活动的学生共有人,估计其中最喜爱“测量”项目的学生人数是多少?23. 如图, , , 平分 . (1)、求的度数;
(1)、求的度数;
(2)、若是从点引出的一条射线,使 , 求的度数.24. 学校要购入两种记录本,预计花费460元,其中A种记录本每本3元,B种记录本每本2元,且购买A种记录本的数量比B种记录本的2倍还多20本.(1)、求购买A和B两种记录本的数量;(2)、某商店搞促销活动,A种记录本按8折销售,B种记录本按9折销售,则学校此次可以节省多少钱?25. 阅读理解:A、、为数轴上三点,若点到的距离是点到的距离倍,我们就称点是【、】的好点,如图 , 点到点的距离是 , 点到点的距离是 , 那么点是【、】的好点,但点不是【、】的好点.
 (1)、知识运用:如图点 【 , 】的好点:请在横线上填“是”或“不”(2)、如图、、为数轴上三点,点所表示的数为 , 点所表示的数为若点是【 , 】的好点,则点所对应的数是多少?
(1)、知识运用:如图点 【 , 】的好点:请在横线上填“是”或“不”(2)、如图、、为数轴上三点,点所表示的数为 , 点所表示的数为若点是【 , 】的好点,则点所对应的数是多少?
(3)、拓展提升:如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点
出发,以每秒个单位的速度向左移动.当经过几秒时,点、点和点中有一个点为其余两点的好点?