重庆市缙云教育联盟2023-2024学年八年级上学期1月期末数学试题
试卷更新日期:2024-01-22 类型:期末考试
一、选择题
-
1. 分式方程的解为( )A、 B、 C、 D、2. 下列变形属于因式分解的是( )A、4x+x=5x B、(x+2)2=x2+4x+4 C、x2+x+1=x(x+1)+1 D、x2﹣3x=x(x﹣3)3. 分式方程的解为( )A、 B、 C、 D、4. △ABC中,∠A= ∠B= ∠C,则△ABC是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、都有可能5. 如图,∠B=40°,∠ACD=108°,若B,C,D三点在一条直线上,则∠A的大小是( )
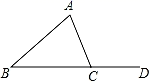 A、148° B、78° C、68° D、50°6. 下列各分式中是最简分式的是( )A、 B、 C、 D、7. 如图,在△ABC中,AB=AC , BD平分∠ABC交AC于D , AE∥BD交CB延长线于点E , 若∠AEB=25°,则∠ADB的度数为( )
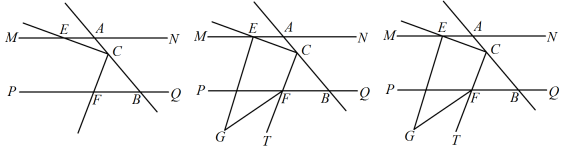
A、148° B、78° C、68° D、50°6. 下列各分式中是最简分式的是( )A、 B、 C、 D、7. 如图,在△ABC中,AB=AC , BD平分∠ABC交AC于D , AE∥BD交CB延长线于点E , 若∠AEB=25°,则∠ADB的度数为( )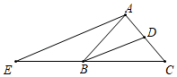 A、50° B、70° C、75° D、80°8. 设为正整数,则存在正整数和 , 使得 , 则、的值分别为( ).A、 , B、 , C、 , D、 ,9. 已知|x|=5,|y|=2,且|x+y|=﹣x﹣y,则x﹣y的值为( )A、±3 B、±3或±7 C、﹣3或7 D、﹣3或﹣710. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )
A、50° B、70° C、75° D、80°8. 设为正整数,则存在正整数和 , 使得 , 则、的值分别为( ).A、 , B、 , C、 , D、 ,9. 已知|x|=5,|y|=2,且|x+y|=﹣x﹣y,则x﹣y的值为( )A、±3 B、±3或±7 C、﹣3或7 D、﹣3或﹣710. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )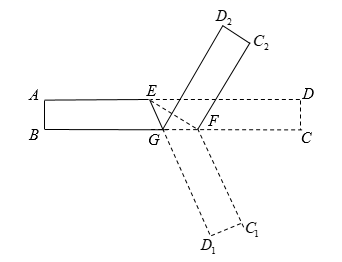 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
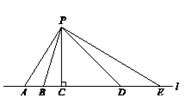
11. 如图,要从村庄P修一条连接公路 的最短的小道,应选择沿线段修建,理由是 .
 12. 计算的结果是 .13. 已知 , 则的值为 .14. 若方程有增根,则 .15. 如图, , 垂足为C , , , 射线 , 垂足为B , 动点P从C点出发以的速度沿射线CQ运动,点N为射线BM上一动点,满足 , 随着P点运动而运动,当点P运动秒时,与点P、N、B为顶点的三角形全等.
12. 计算的结果是 .13. 已知 , 则的值为 .14. 若方程有增根,则 .15. 如图, , 垂足为C , , , 射线 , 垂足为B , 动点P从C点出发以的速度沿射线CQ运动,点N为射线BM上一动点,满足 , 随着P点运动而运动,当点P运动秒时,与点P、N、B为顶点的三角形全等.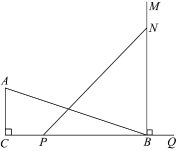 16. 如图,现有边长分别为和的正方形纸片,以及长、宽分别为的长方形,其中 . 将两正方形纸片按图1和图2两种方式(图1和图2中两张正方形纸片均有部分重叠)放置于长方形中,其中未被覆盖的部分用阴影表示.若图1中阴影部分的面积记为 , 图2中阴影部分的面积记为 . 则 .
16. 如图,现有边长分别为和的正方形纸片,以及长、宽分别为的长方形,其中 . 将两正方形纸片按图1和图2两种方式(图1和图2中两张正方形纸片均有部分重叠)放置于长方形中,其中未被覆盖的部分用阴影表示.若图1中阴影部分的面积记为 , 图2中阴影部分的面积记为 . 则 .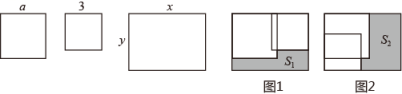 17. 若关于x的不等式组的解集为 , 且关于y的分式方程有非负整数解,则所有满足条件的整数m的值的和是 .18. 已知 , , 且< , 则的值是.
17. 若关于x的不等式组的解集为 , 且关于y的分式方程有非负整数解,则所有满足条件的整数m的值的和是 .18. 已知 , , 且< , 则的值是.三、解答题
-
19.(1)、计算:(2)、先化简,再求值: , 其中 .20. 如图,已知, , 点D、E分别在、上,且 , , 连接 , 、交于点M、连接 .
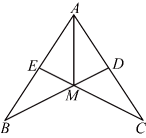 (1)、求证:;(2)、嘉琪说:“若 , 则E是的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.21. 如图,在中,的角平分线交于点D .
(1)、求证:;(2)、嘉琪说:“若 , 则E是的中点”,请你运用所学知识判断嘉琪的说法是否正确,若正确,给出证明;若不正确,说出理由.21. 如图,在中,的角平分线交于点D . (1)、用尺规完成以下基本作图:作的垂直平分线分别与、、交于点E、点F、点H . (保留作图痕迹,不写作法)(2)、在(1)所作的图形中,连接、 , 完成下面证明的过程.
(1)、用尺规完成以下基本作图:作的垂直平分线分别与、、交于点E、点F、点H . (保留作图痕迹,不写作法)(2)、在(1)所作的图形中,连接、 , 完成下面证明的过程.证明:∵的角平分线交于点D ,
∴ ▲ .
∵垂直平分 ,
∴ , ▲ , ▲ ,
∴ ,
∴ ,
∴ ▲ .
∴ .
22. 我们约定:若关于的整式与同时满足: , , 则称整式A与整式互为“美美与共”整式.根据该约定,解答下列问题:(1)、若关于的整式与互为“美美与共”整式,求k , m , n的值.(2)、若关于x的整式 , (a , b为常数),M与互为“美美与共”整式,且是的一个因式,求的值;(3)、若 , 且关于的方程的解为正整数,求的“美美与共”整式 , 并求出的最小值.