重庆市缙云教育联盟2023-2024学年七年级上学期1月期末数学试题
试卷更新日期:2024-01-22 类型:期末考试
一、选择题
-
1. 把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是( )A、 B、 C、 D、2. 分数的倒数是( )A、 B、 C、 D、33. 定义一种新运算: , 则的是( )A、 B、1 C、3 D、24. 根据国家统计局统计,2023年前三季度,夏粮早稻实现增产,全国夏粮早稻产量合计3511亿斤,秋粮生产总体稳定,从收获的情况看,全年粮食有望再获丰收.数据“3511亿”用科学记数法表示为( )A、 B、 C、 D、5. 数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2008厘米的线段AB , 则线段AB盖住的整点是( )A、2006个或2007个 B、2007个或2008个 C、2008个或2009个 D、2009个或2010个6. 一个自行车队进行训练,训练时所有队员都以40km/h的速度前进,突然,6号队员以50km/h的速度独自行进,行进15km后掉转车头,仍以50km/h的速度往回骑,直到与其他队员会合.设6号队员从离队开始到与队员重新会合经过了xh,则x为( )A、1.5 B、0.5 C、 D、7. 如图:正方形的边长与圆半径都是 , 则图中阴影部分的面积是( )cm2
 A、 B、 C、 D、8. 若= , 则的值可表示为( )A、 B、 C、 D、9. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )
A、 B、 C、 D、8. 若= , 则的值可表示为( )A、 B、 C、 D、9. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )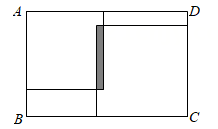 A、 B、 C、 D、10. 下列说法正确的个数有( )①已知且则数在数轴上距离原点较近的是②若一个数小于它的绝对值,则这个数是负数;③一定是负数;④若则是非正数.A、4个 B、3个 C、2个 D、1个
A、 B、 C、 D、10. 下列说法正确的个数有( )①已知且则数在数轴上距离原点较近的是②若一个数小于它的绝对值,则这个数是负数;③一定是负数;④若则是非正数.A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 赤峰市某天早晨的气温是 , 到中午时升高了 , 那么中午的温度是 .12. 若1<a<2,化简 的结果是.13. 在2x2y、﹣2xy2、﹣3x2y、xy四个代数式中,找出两个同类项,并合并这两个同类项得 .14. 如图,点是线段的中点,点在线段上,且 , , 则线段的长为 .
 15. 若 的补角比其余角的2倍大30°,则 的度数为.16. 观察下列式子:;;;;…根据上述规律,计算:.17. 甲乙两城市相距420千米,客车与轿车分别从甲乙两城市同时出发,相向而行.已知客车每小时行70千米,轿车每小时行110千米,经过小时客车与轿车相距60千米.18. 如图,将正整数从点O开始,依次按如图所示的方式在格点(横线和竖线的交点)上排布,点O表示的数是1,第1个拐角处点表示的数是2,第2个拐角处点表示的数是3,第3个拐角处点表示的数是7,第4个拐角处点表示的数是9,……,那么第201个拐角处点表示的数是 .
15. 若 的补角比其余角的2倍大30°,则 的度数为.16. 观察下列式子:;;;;…根据上述规律,计算:.17. 甲乙两城市相距420千米,客车与轿车分别从甲乙两城市同时出发,相向而行.已知客车每小时行70千米,轿车每小时行110千米,经过小时客车与轿车相距60千米.18. 如图,将正整数从点O开始,依次按如图所示的方式在格点(横线和竖线的交点)上排布,点O表示的数是1,第1个拐角处点表示的数是2,第2个拐角处点表示的数是3,第3个拐角处点表示的数是7,第4个拐角处点表示的数是9,……,那么第201个拐角处点表示的数是 .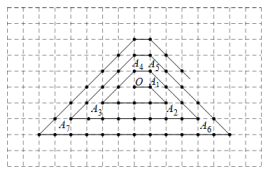
三、解答题
-
19. 先化简,再求值: , 其中x , y满足 .20. 某检修小组开车从单位出发,检修东西走向的供电线路,规定向东为正,向西为负,一天的行程是(单位:千米): , , , , , , 4, , 16, .(1)、最后他们是否回到出发点?若没有,则在出发点的什么方向?距离出发点多远?(2)、若汽车耗油量为升千米,检修小组完成工作返回出发地,则他们该天共耗油多少升?21. 阅读解方程的途径.
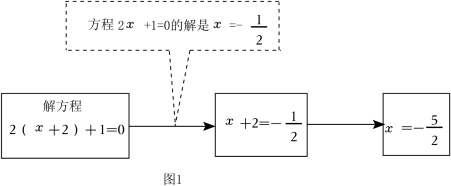
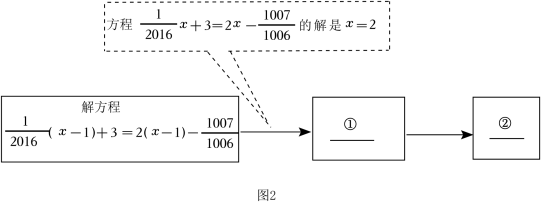 (1)、按照图1所示的途径,填写图2内空格.
(1)、按照图1所示的途径,填写图2内空格.①;② .
(2)、已知关于x的方程+c=的解是或(a、b、c均为常数).求关于x的方程+c=(k、m为常数,)的解(用含k、m的代数式表示).22. 已知数轴上 , , 三个点表示的数分别是 , , 且满足 , 动点、都从点出发,且点以每秒1个单位长度的速度向终点移动. (1)、直接写出 , , ;(2)、若为的中点,为的中点,试判断在点运动的过程中,线段的长度是否发生变化,请说明理由;(3)、当点运动到点时,点再从点出发,以每秒3个单位长度的速度在 , 之间往返运动,直至点停止运动,点也停止运动.当点开始运动后的第秒时, , 两点之间的距离为4.(直接写出答案)23. 如图,某校的饮水机有温水、开水两个按钮.温水和开水公用一个出水口.温水的温度为 , 流速为;开水的温度为 , 流速为.整个接水的过程不计热量损失.
(1)、直接写出 , , ;(2)、若为的中点,为的中点,试判断在点运动的过程中,线段的长度是否发生变化,请说明理由;(3)、当点运动到点时,点再从点出发,以每秒3个单位长度的速度在 , 之间往返运动,直至点停止运动,点也停止运动.当点开始运动后的第秒时, , 两点之间的距离为4.(直接写出答案)23. 如图,某校的饮水机有温水、开水两个按钮.温水和开水公用一个出水口.温水的温度为 , 流速为;开水的温度为 , 流速为.整个接水的过程不计热量损失. (1)、用空杯先接温水,再接开水,接完后杯中共有水 , 水温为 .(2)、某学生先接了一会温水,又接了一会开水,得到一杯温度为的水.设该学生接温水的时间为 , 请求出的值;(3)、研究表明,蜂蜜的最佳冲泡温度是 , 某教师携带一个容量为的水杯接水,用来泡蜂蜜,要使接满水时杯中水温在最佳冲泡温度范围内,请直接写出该教师分配接水时间的方案(接水时间按整秒计算).24. 如图(1)所示,线段与线段重合,点是它们的中点,保持不动,将绕点顺时针旋转);射线从与射线重合开始,绕点逆时针旋转(至多旋转到与射线重合为止).
(1)、用空杯先接温水,再接开水,接完后杯中共有水 , 水温为 .(2)、某学生先接了一会温水,又接了一会开水,得到一杯温度为的水.设该学生接温水的时间为 , 请求出的值;(3)、研究表明,蜂蜜的最佳冲泡温度是 , 某教师携带一个容量为的水杯接水,用来泡蜂蜜,要使接满水时杯中水温在最佳冲泡温度范围内,请直接写出该教师分配接水时间的方案(接水时间按整秒计算).24. 如图(1)所示,线段与线段重合,点是它们的中点,保持不动,将绕点顺时针旋转);射线从与射线重合开始,绕点逆时针旋转(至多旋转到与射线重合为止).在此基础上,我们给出如下定义:比较与的大小,若 , 则将其中较小角的度数定义为对的“迷你角度”;若 , 则将或的度数定义为对的“迷你角度”.
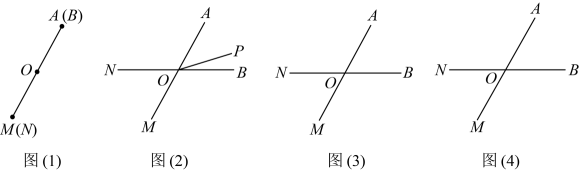 (1)、当时,
(1)、当时,①如图(2)所示,若 , 求对的“迷你角度”是多少度;
②若对的“迷你角度”为 , 请借助图(3)和图(4)进行分析,求出的值是多少.
(2)、若时,对的“迷你角度”是 , 请直接写出的值,不用说明理由.