人教版初中数学2023-2024学年九年级下学期课时培优练习 27.2相似三角形
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 如图, , , 点A在上, , 的平分线交于M , 交于P , 连接交于点N , 以下四个结论:①;②;③四边形的面积是面积的一半;④ . 一定正确的有( )个.
 A、1 B、2 C、3 D、42. 如图,在正方形中,点分别是边上的两点,且分别交于 . 对于下列结论:
A、1 B、2 C、3 D、42. 如图,在正方形中,点分别是边上的两点,且分别交于 . 对于下列结论:①;②;③;④当时,面积的最小值为 . 其中正确的是( )
 A、①② B、②③ C、①②③ D、①②③④3. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( )
A、①② B、②③ C、①②③ D、①②③④3. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( ) A、 B、2 C、 D、4. 如图,点 , , 分别在的边上, , , , 点是的中点,连接并延长交于点 , 的值是( ).
A、 B、2 C、 D、4. 如图,点 , , 分别在的边上, , , , 点是的中点,连接并延长交于点 , 的值是( ).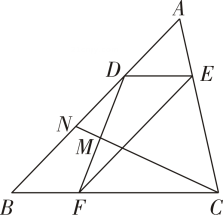 A、 B、 C、 D、5. 如图,把菱形向平移至的位置,作 , 垂足为与相交于点的延长线交于点 , 连接 , 则下列结论:①;②;③;④ , 则正确的结论有( )个
A、 B、 C、 D、5. 如图,把菱形向平移至的位置,作 , 垂足为与相交于点的延长线交于点 , 连接 , 则下列结论:①;②;③;④ , 则正确的结论有( )个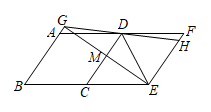 A、1 B、2 C、3 D、46. 如图,M是正方形的边上中点,点E、F分别在边上,且 . ① , ②是的比例中项,③平分 , ④ . 上述四个判断中正确的有( )个.
A、1 B、2 C、3 D、46. 如图,M是正方形的边上中点,点E、F分别在边上,且 . ① , ②是的比例中项,③平分 , ④ . 上述四个判断中正确的有( )个. A、1 B、2 C、3 D、47. 如图,在正方形中,是等边三角形,、的延长线分别交于点 , , 连接、 , 与相交于点 , 给出下列结论:①;②;③;④;⑤ . 其中正确结论的个数是( )
A、1 B、2 C、3 D、47. 如图,在正方形中,是等边三角形,、的延长线分别交于点 , , 连接、 , 与相交于点 , 给出下列结论:①;②;③;④;⑤ . 其中正确结论的个数是( ) A、5 B、4 C、3 D、28. 如图△ABC中,∠ACB=90°,AB=4,AC=x , ∠BAC=α,O为AB中点,若点D为直线BC下方一点,且△BCD与△ABC相似,则下列结论:
A、5 B、4 C、3 D、28. 如图△ABC中,∠ACB=90°,AB=4,AC=x , ∠BAC=α,O为AB中点,若点D为直线BC下方一点,且△BCD与△ABC相似,则下列结论:
①若α=60°,则AD的最大值为;
②若α=60°,△ABC∽△CBD , 则OD的长为;
③若α=45°,BC与OD相交于E , 则点E不一定是△ABD的重心;
④若△ABC∽△BCD , 则当x=2时,AC+CD取得最大值.其中正确的为( )
A、①③ B、①②④ C、③④ D、①③④9. 如图①,在△ABC中,∠B=108°,动点P从点A出发,沿折线A→B→C→A匀速运动一周.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为v(cm),v与t的函数图象如图②所示.当BP恰好是∠ABC的一条三等分线时,t的值为( ) A、+2或5 B、+3或6 C、+3或5 D、+2或610. 如图,矩形ABCD中, , , EF是对角线BD的垂直平分线,则EF的长为( )
A、+2或5 B、+3或6 C、+3或5 D、+2或610. 如图,矩形ABCD中, , , EF是对角线BD的垂直平分线,则EF的长为( ) A、 B、5cm C、 D、8cm
A、 B、5cm C、 D、8cm二、填空题
-
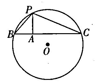
11. 如图,⊙O的半径为10,点P在⊙O上,点A在⊙O内,且AP=6,过点A作AP的垂线交QO于点B,C.若PC=15,则PB=.
 12. 如图,在中, , 以点B为圆心,BD长为半径作圆,点E为⊙B上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF,当点E与点D重合时,BF的值为 , 点E在⊙B上运动过程中,BF存在最大值为 .
12. 如图,在中, , 以点B为圆心,BD长为半径作圆,点E为⊙B上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF,当点E与点D重合时,BF的值为 , 点E在⊙B上运动过程中,BF存在最大值为 .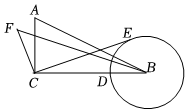 13. 如图,在矩形ABCD中,AB=3,AD=6,点E、F分别是AB、BC边上的动点,且AE:BF=2:1,连接AF和DE交于点G , 连接CG , 则CG的最小值是 .
13. 如图,在矩形ABCD中,AB=3,AD=6,点E、F分别是AB、BC边上的动点,且AE:BF=2:1,连接AF和DE交于点G , 连接CG , 则CG的最小值是 . 14. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移a个单位长度(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的值为
14. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移a个单位长度(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的值为 15. 如图,在△ABC中,AB=AC=4,AF⊥BC于点F,BH⊥AC于点H.交AF于点G,点D在直线AF上运动,BD=DE,∠BDE=135°,∠ABH=45°,当AE取最小值时,BE的长为.
15. 如图,在△ABC中,AB=AC=4,AF⊥BC于点F,BH⊥AC于点H.交AF于点G,点D在直线AF上运动,BD=DE,∠BDE=135°,∠ABH=45°,当AE取最小值时,BE的长为.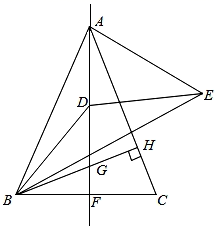
三、解答题
-
16. 如图1,内接于圆为直径,点在的上方,且 . 连结是边上的高,过点作交的延长线于点 , 交于点 .
 (1)、求证: .(2)、当时,求的值.(3)、如图2,取的中点 , 连结 .
(1)、求证: .(2)、当时,求的值.(3)、如图2,取的中点 , 连结 .①若 , 在点运动的过程中,当四边形的其中一边长是的2倍时,求所有满足条件的的长.
②连结 , 当的面积是的面积的2倍时,则 ▲ (请直接写出答案)
17. 如图所示,中, , , .点从点开始沿边向以1cm/s的速度移动,点从点开始沿边向点以2cm/s的速度移动. , 分别从 , 同时出发. (1)、经过几秒,、间的距离等于6cm?(2)、线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,说明理由.(3)、几秒时,与相似?18. 如图,AB为⊙O的切线,B为切点,过点B作BC⊥OA , 垂足为点E , 交⊙O于点C , 连接CO并延长CO与AB的延长线交于点D , 连接AC .
(1)、经过几秒,、间的距离等于6cm?(2)、线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,说明理由.(3)、几秒时,与相似?18. 如图,AB为⊙O的切线,B为切点,过点B作BC⊥OA , 垂足为点E , 交⊙O于点C , 连接CO并延长CO与AB的延长线交于点D , 连接AC . (1)、求证:AC为⊙O的切线;(2)、若⊙O半径为3,OD=5.求线段AD的长.19. 如图,AD是ΔABC的外角∠EAC的平分线,与ΔABC的外接圆⊙O交于点D,连结BD交AC于点F.
(1)、求证:AC为⊙O的切线;(2)、若⊙O半径为3,OD=5.求线段AD的长.19. 如图,AD是ΔABC的外角∠EAC的平分线,与ΔABC的外接圆⊙O交于点D,连结BD交AC于点F. (1)、求证:(2)、若BC=3.当AF将ΔABD的面积分为1:2两部分时,求ΔADF与ΔBCF的面积比值.(3)、将C点关于AD的对称点记为点C',当BD时,写出AD与半径r的数量关系,并说明理由.20. 在矩形ABCD中,点E为AB边上一动点(不与点A , B重合),连接CE , 过点E作EF⊥CE . 连接AC、AF、CF , CF与EF分别交AD于点G , H .
(1)、求证:(2)、若BC=3.当AF将ΔABD的面积分为1:2两部分时,求ΔADF与ΔBCF的面积比值.(3)、将C点关于AD的对称点记为点C',当BD时,写出AD与半径r的数量关系,并说明理由.20. 在矩形ABCD中,点E为AB边上一动点(不与点A , B重合),连接CE , 过点E作EF⊥CE . 连接AC、AF、CF , CF与EF分别交AD于点G , H .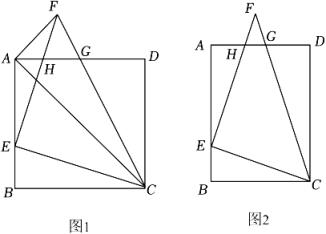 (1)、如图1,当矩形ABCD为正方形时,且EF=CE . 求证:△BCE∽△ACF;(2)、在(1)的条件下,且点E为AB的中点,求的值;(3)、如图2,已知:AB=8,BC=6, , 连接CF交AD于G , EF与AD交于H , 若FG=FH , 求BE的长度.
(1)、如图1,当矩形ABCD为正方形时,且EF=CE . 求证:△BCE∽△ACF;(2)、在(1)的条件下,且点E为AB的中点,求的值;(3)、如图2,已知:AB=8,BC=6, , 连接CF交AD于G , EF与AD交于H , 若FG=FH , 求BE的长度.