人教版初中数学2023-2024学年九年级下学期课时基础练习 27.2相似三角形
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1.
如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( )
 A、∠B=∠ACD B、∠ADC=∠ACB C、= D、AC2=AD•AB2. 已知△ABC∽△DEF,AB:DE=1:2,则△ABC与△DEF的周长比等于( )
A、∠B=∠ACD B、∠ADC=∠ACB C、= D、AC2=AD•AB2. 已知△ABC∽△DEF,AB:DE=1:2,则△ABC与△DEF的周长比等于( )
A、1:2 B、1:4 C、2:1 D、4:13. 已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )A、2cm,3cm B、4cm,5cm C、5cm,6cm D、6cm,7cm4. 如图,△ABC内接于⊙O,若AB= , AC= , BC=7,则⊙O的半径是( )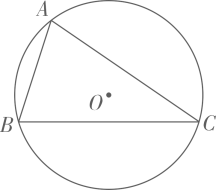 A、 B、 C、 D、5. 如图,已知 , 点是边中点,且若 , 则( )
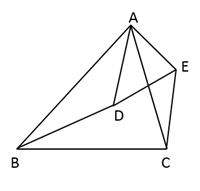
A、 B、 C、 D、5. 如图,已知 , 点是边中点,且若 , 则( )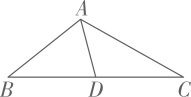 A、3 B、4 C、 D、6. 如图,四边形ABCD内接于.于点M,.设 , , , , 则下列为定值的是( )
A、3 B、4 C、 D、6. 如图,四边形ABCD内接于.于点M,.设 , , , , 则下列为定值的是( ) A、 B、 C、 D、7. 有一块锐角三角形余料 , 边的长为 , 边上的高为 , 现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A、 B、 C、 D、7. 有一块锐角三角形余料 , 边的长为 , 边上的高为 , 现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( ) A、5个 B、6个 C、7个 D、8个8. 如图,在等腰直角三角形中, , .点是上一点, , 过点作 , 交于点.则为( )
A、5个 B、6个 C、7个 D、8个8. 如图,在等腰直角三角形中, , .点是上一点, , 过点作 , 交于点.则为( )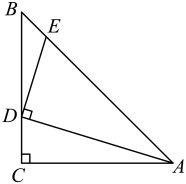 A、 B、 C、 D、9. 如图,在平面直角坐标系中,已知A(-2,4)、P(-1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则PM的最小值为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,已知A(-2,4)、P(-1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则PM的最小值为( )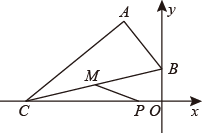 A、 B、 C、 D、10. 如图,直线 , 直线 , 分别交 , , 于点 , , 和点 , , , 连结.作 , 若 , , 则的长为( )
A、 B、 C、 D、10. 如图,直线 , 直线 , 分别交 , , 于点 , , 和点 , , , 连结.作 , 若 , , 则的长为( ) A、12 B、13 C、14 D、15
A、12 B、13 C、14 D、15二、填空题
-
11. 若两个相似三角形的周长比是4:9,则对应中线的比是 .12. 如果两个相似三角形的周长比为1:2,那么它们的对应中线的比为.13. 如图,利用标杆测量楼高,点A,D,B在同一直线上, , , 垂足分别为E,C.若测得 , , , 则楼高m.
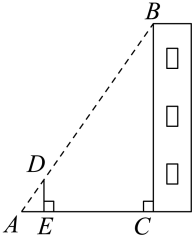 14. 如图,在等腰中, , , 在上,且 , 则 .
14. 如图,在等腰中, , , 在上,且 , 则 . 15. 如图,已知在△ABC中,D,E分别是AB,AC上的点, , .若DE=2,则BC的长是.
15. 如图,已知在△ABC中,D,E分别是AB,AC上的点, , .若DE=2,则BC的长是.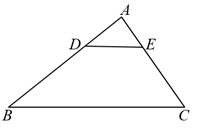
三、解答题
-
16. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上、已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
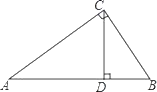
 17. 已知如图,Rt△ABC中,∠C=90°,CD是斜边上的高,求证:CD2=AD•BD.
17. 已知如图,Rt△ABC中,∠C=90°,CD是斜边上的高,求证:CD2=AD•BD.