人教版初中数学2023-2024学年九年级下学期课时培优练习 27.1图形的相似
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 将一张()纸片,以它的一边为边长剪去一个菱形,将余下的平行四边形中,再以它的一边为边长剪去一个菱形,若剪去两个菱形后所剩下的平行四边形与原来相似,则的相邻两边与的比值是( )A、 B、 C、或 D、或或2. 如图,E,F,G,H分别是矩形四条边上的点,连接相交于点I,且 , , 矩形矩形 , 连接交于点P,Q,下列一定能求出面积的条件是( )
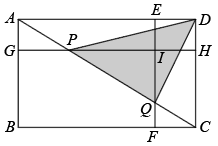 A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差3. 如图, , , , 是正方形边上的点,且 , 和将正方形剪切成四片进行重新拼接成四边形 , 若正方形和四边形的面积之比为 , 则( )
A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差3. 如图, , , , 是正方形边上的点,且 , 和将正方形剪切成四片进行重新拼接成四边形 , 若正方形和四边形的面积之比为 , 则( )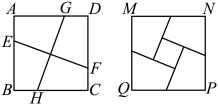 A、2 B、3 C、 D、4. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、2 B、3 C、 D、4. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )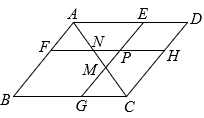 A、 B、 C、 D、5. 如图,菱形ABCD沿对角线AC的方向平移到菱形A'B′C′D′的位置,点A′恰好是AC的中点.若菱形ABCD的边长为2,∠BCD=60°,则阴影部分的面积为( )
A、 B、 C、 D、5. 如图,菱形ABCD沿对角线AC的方向平移到菱形A'B′C′D′的位置,点A′恰好是AC的中点.若菱形ABCD的边长为2,∠BCD=60°,则阴影部分的面积为( )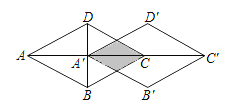 A、 B、 C、1 D、6. 如图,P为反比例函数y= (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( )
A、 B、 C、1 D、6. 如图,P为反比例函数y= (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( ) A、2 B、4 C、6 D、87. 下列说法不一定正确的是( )A、所有的等边三角形都相似 B、所有的等腰直角三角形都相似 C、所有的菱形都相似 D、所有的正方形都相似8. 如图,BD是的对角线,BD⊥AD,AB=2AD=6,点E是CD的中点,点F、P分别是线段AB、BD上的动点,若△ABD∽△PBF,且△PDE是等腰三角形,则PF的长为( )
A、2 B、4 C、6 D、87. 下列说法不一定正确的是( )A、所有的等边三角形都相似 B、所有的等腰直角三角形都相似 C、所有的菱形都相似 D、所有的正方形都相似8. 如图,BD是的对角线,BD⊥AD,AB=2AD=6,点E是CD的中点,点F、P分别是线段AB、BD上的动点,若△ABD∽△PBF,且△PDE是等腰三角形,则PF的长为( ) A、或 B、或 C、或 D、或9. 要拼出和图①中的菱形相似的较长对角线为88cm的大菱形(如图②) ,需要如图①的菱形的个数是( ).
A、或 B、或 C、或 D、或9. 要拼出和图①中的菱形相似的较长对角线为88cm的大菱形(如图②) ,需要如图①的菱形的个数是( ). A、11个 B、121个 C、22个 D、242 个10. 若一个矩形剪掉一个面积最大的正方形,剩下的小矩形与原来的矩形相似,且原矩形的较长边长为 , 则剩下的小矩形的较短边长为( )A、 B、 C、 D、
A、11个 B、121个 C、22个 D、242 个10. 若一个矩形剪掉一个面积最大的正方形,剩下的小矩形与原来的矩形相似,且原矩形的较长边长为 , 则剩下的小矩形的较短边长为( )A、 B、 C、 D、二、填空题
-
11. 如图所示,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 , 则的值为.
 12. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
12. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .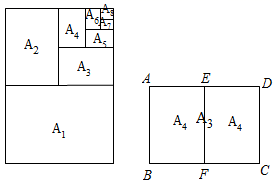 13. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是.
13. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是. 14. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .
14. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .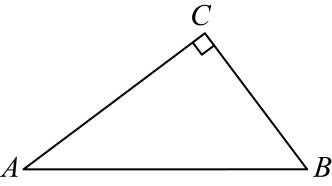 15. 某地为了更好地保护红军历史博物馆,经过精心的筹备规划,决定把原来博物馆的平面图扩大.如图,已知原来博物馆的平面图是 ,规划后博物馆的平面图是四边形 ,其中点A,B,C,D分别是边 的中点.如果原来博物馆的平面图 的面积为 ,则规划后博物馆的平面图 占地面积为 .
15. 某地为了更好地保护红军历史博物馆,经过精心的筹备规划,决定把原来博物馆的平面图扩大.如图,已知原来博物馆的平面图是 ,规划后博物馆的平面图是四边形 ,其中点A,B,C,D分别是边 的中点.如果原来博物馆的平面图 的面积为 ,则规划后博物馆的平面图 占地面积为 .
三、解答题
-
16. 如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
 17. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
17. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少? 18.
18.如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是多少?
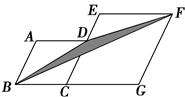 19.
19.八年级数学学习合作小组在学过《图形的相似》这一章后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.如:我们可以定义:“长和宽之比相等的矩形是相似矩形.”相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长比等于相似比,面积比等于相似比的平方等等.请你参与这个学习小组,一同探索这类问题:

(1)写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
(2)如图,将菱形ABCD沿着直线AC向右平移后得到菱形A′B′C′D′,试证明:四边形A′FCE是菱形,且菱形ABCD∽菱形A′FCE;
(3)若AC= , 菱形A′FCE的面积是菱形ABCD面积的一半,求平移的距离AA′的长.20.如图,An系列矩形纸张的规格特征是:①各矩形纸张都相似;②A1纸对裁后可以得到两张A2纸,A2纸对裁后可以得到两张A3纸,…,An纸对裁后可以得到两张An+1纸.
(1)填空:A1纸面积是A2纸面积的几倍,A2纸周长是A4纸周长的几倍;
(2)根据An系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比;
(3)设A1纸张的重量为a克,试求出A8纸张的重量.(用含a的代数式表示)
