人教版初中数学2023-2024学年九年级下学期课时基础练习 26.2实际问题与反比例函数

试卷更新日期：2024-01-20 类型：同步测试

进入出卷网下载

一、选择题

1. 近视眼镜的度数 $y$ （度）与镜片焦距 $x$ （m）成反比例，已知200度近视眼镜的镜片焦距为0.5m，若某近视眼镜片的焦距为0.25m，则该眼镜片的度数为（）

A、100度 B、300度 C、400度 D、600度

查看试题解析
2. 某厂现有300吨煤，这些煤能烧的天数 $y$ 与平均每天烧的吨数 $x$ 之间的函数关系是（）

A、 $y = \frac{300}{x} (x > 0)$ B、 $y = \frac{300}{x} (x \geq 0)$ C、 $y = 300 x (x \geq 0)$ D、 $y = 300 x (x > 0)$

查看试题解析
3. 如图， $A$ ， $B$ 是反比例函数 $y = \frac{4}{x}$ 在第一象限内的图象上的两点，且 $A$ ， $B$ 两点的横坐标分别是2和4，则 $△ O A B$ 的面积是（）

A、3 B、2 C、 $3.5$ D、4

查看试题解析
4. 菱形的面积为2，其对角线分别为x、y，则y与x的图象大致（）．

A、 B、 C、 D、

查看试题解析
5. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强 $p (P a)$ 是气球体积 $V (m^{3})$ 的反比例函数，其图像如图所示.当气球内的气压大于 $40000 P a$ 时，气球将爆炸，为确保气球不爆炸，气球的体积应（）

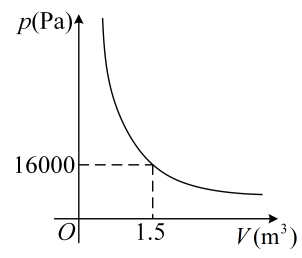A、不小于 $0.06 m^{3}$ B、不大于 $0.06 m^{3}$ C、不小于 $0.6 m^{3}$ D、不大于 $0.6 m^{3}$

查看试题解析
6. 对于反比例函数 $y = - \frac{2}{x}$ ，下列说法不正确的是（）

A、点 $(- 2 ， 1)$ 在它的图象上 B、它的图象在第二、四象限 C、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 D、当 $x < 0$ 时， $y$ 随 $x$ 的增大而减小

查看试题解析
7. 如图，某加油站计划在地下修建一个容积为 $2 \times 1 0^{4} m^{3}$ 的圆柱形石油储存室，则储存室的底面积S（单位： $m^{2}$ ）与其深度h（单位：m）的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 某电子产品的售价为8000元，购买该产品时可分期付款：前期付款3000元，后期每个月分别付相同的数额，则每个月付款额y（元）与付款月数x（x为正整数）之间的函数关系式是（）

A、 $y = \frac{8000}{x} - 3000$ B、 $y = \frac{8000}{x} + 3000$ C、 $y = \frac{3000}{x}$ D、 $y = \frac{5000}{x}$

查看试题解析
9. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m，则动力F(单位：N)关于动力臂l(单位：m)的函数表达式正确的是（）

A、 $F = \frac{1200}{l}$ B、 $F = \frac{600}{l}$ C、 $F = \frac{500}{l}$ D、 $F = \frac{0.5}{l}$

查看试题解析
10. 某工厂现有原材料100吨，每天平均用去x吨，这批原材料能用y天，则y与x之间的函数表达式为（）

A、 $y = 100 x$ B、 $y = \frac{100}{x}$ C、 $y = \frac{x}{2} + 100$ D、 $y = 100 - x$

查看试题解析

二、填空题

11. 列车从甲地驶往乙地．行完全程所需的时间 $t (h)$ 与行驶的平均速度 $v (k m / h)$ 之间的反比例函数关系如图所示．若列车要在 $2.5 h$ 内到达，则速度至少需要提高到 $k m / h$ ．

查看试题解析
12. 一个游泳池的容积为 $2000 m^{3}$ ，游泳池注满水所用时间 $t$ 与注水速度 $v$ （填“成正比例”、“成反比例”、“不成比例”）．

查看试题解析
13. 为预防流感，某学校对教室进行“药熏消毒”．消毒期间，室内每立方米空气中的含药量y（mg）与时间x（min）之间的函数关系如图所示．已知在药物燃烧阶段，y与x成正比例，燃烧完后y与x成反比例．现测得药物10min燃烧完，此时教室内每立方米空气含药量8mg ，当每立方米空气中含药量低于1.6mg时，对人体无毒害作用．那么从消毒开始，经过min后教室内的空气才能达到安全要求．

查看试题解析
14. 如图，点A（0，1），B（-2，0），以AB为边在第二象限作矩形ABCD，反比例函数y= $\frac{k}{x}$ 的图象经过点C．若矩形ABCD的面积为10，则k的值为

查看试题解析
15. 当三角形的面积为9cm²时，它的底边长a（cm）与底边上的高h（cm）之间的函数表达式为．

查看试题解析

三、解答题

16. 已知反比例函数 $y = \frac{2 - k}{x}$ 的图象经过点 $A (3 ， - 2)$ .

(1)、求k的值；

(2)、点 $C (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 均在反比例函数 $y = \frac{2 - k}{x}$ 的图象上，若 $0 < x_{1} < x_{2}$ ，直接写出 $y_{1}$ ， $y_{2}$ 的大小关系.

查看试题解析
17. 某人采用药薰消毒法进行消毒．已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧后y与x成反比例（如图所示），现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg ，请你根据题中所提供的信息，解答下列问题．

(1)、药物燃烧时y关于x的函数关系式为，自变量x的取值范围是；药物燃烧后y与x的函数关系式为．

(2)、研究表明，当空气中每立方米的含药量低于1.6mg时学生可以进教室，那么从消毒开始，至少多少分钟后学生才能回到教室？

(3)、研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，此次消毒是否有效？为什么？

查看试题解析
18. 某蔬菜生产基地用装有恒温系统的大棚栽培一种新品，如图是某天恒温系统从开始到关闭及关闭后，大棚里温度 $y (℃)$ 随时间 $x (h)$ 变化的函数图象，其中 $A B$ 段是恒温阶段， $B C$ 段是双曲线 $y = \frac{k}{x}$ 的一部分，请根据图中信息解答下列问题：

(1)、求 $k$ 的值；

(2)、恒温系统在一天内保持大棚内温度不低于 $15 ℃$ 的时间有多少小时？

查看试题解析
19. 某校科技小组在一次野外考察中遇到一片烂泥湿地 $.$ 为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木板，构筑成一条临时近道 $.$ 每块木板对地面的压强 $p (P a)$ 是木板面积 $S (m^{2})$ 的反比例函数，其图象如图所示．

(1)、请根据图象直接写出反比例函数的解析式；

(2)、如果要求压强不超过 $8000 P a$ ，求选用的木板的面积至少要多大？

查看试题解析
20. 甲工程队新建公路，每名工人每天工作8小时，则甲工程队每天可完成600米新建公路．乙工程队比甲工程队少10名工人，每名工人每天工作10小时，则乙工程队每天可完成500米新建公路，假定甲、乙两工程队的每名工人每小时完成的工作量相同，求乙工程队的工人有多少名？

查看试题解析