人教版初中数学2023-2024学年九年级下学期课时培优练习 26.1反比例函数
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 函数图象与有交点 , 且满足 , 则的取值范围是( )A、 B、或2 C、 D、或2. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)3. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、4. 如图,反比例函数的图像上有一点 , 轴于点 , 点在轴上,则的面积为( )
 A、1 B、2 C、4 D、85. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A、1 B、2 C、4 D、85. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )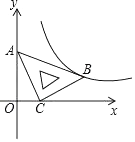 A、( ,0) B、(2,0) C、( ,0) D、(3,0)6. 反比例函数图象上有两点 , 若 , 则的值为( ).A、-1 B、0 C、1 D、27. 已知一次函数的图象如图所示,则的图象是( )
A、( ,0) B、(2,0) C、( ,0) D、(3,0)6. 反比例函数图象上有两点 , 若 , 则的值为( ).A、-1 B、0 C、1 D、27. 已知一次函数的图象如图所示,则的图象是( )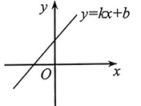 A、
A、 B、
B、 C、
C、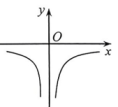 D、
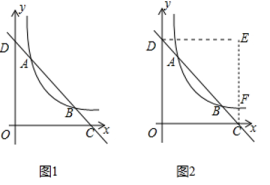
D、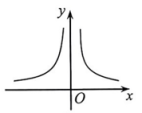 8. 如图,在平面直角坐标系中,的顶点C , A分别在x轴,y轴上, , , 且斜边轴.若反比例函数的图象恰好经过的中点D , 则k的值为( )
8. 如图,在平面直角坐标系中,的顶点C , A分别在x轴,y轴上, , , 且斜边轴.若反比例函数的图象恰好经过的中点D , 则k的值为( ) A、 B、 C、 D、9. 如图,点A在函数y=(x>0)的图象上,点B在函数y=(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C , 则四边形ABCO的面积为( )
A、 B、 C、 D、9. 如图,点A在函数y=(x>0)的图象上,点B在函数y=(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C , 则四边形ABCO的面积为( ) A、1 B、2 C、3 D、410. 函数与在同一直角坐标系中的图像可能是( )A、
A、1 B、2 C、3 D、410. 函数与在同一直角坐标系中的图像可能是( )A、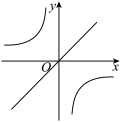 B、
B、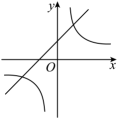 C、
C、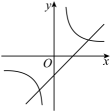 D、
D、
二、填空题
-
11. 双曲线和如图所示,是双曲线上一点,过点作轴,垂足为 , 交双曲线于点 , 连接 , 若的面积为2,则 .
 12. 已知函数y=(m+3)x|m|﹣4是反比例函数,则m= .13. 如图,点P是双曲线上的一点,点A,B是x轴正半轴上的不同点,连接AP,BP,已知 , , 的面积为3,则 .
12. 已知函数y=(m+3)x|m|﹣4是反比例函数,则m= .13. 如图,点P是双曲线上的一点,点A,B是x轴正半轴上的不同点,连接AP,BP,已知 , , 的面积为3,则 . 14. 如图,正方形四个顶点分别位于两个反比例函数和的图象的四个分支上,则n的值= .
14. 如图,正方形四个顶点分别位于两个反比例函数和的图象的四个分支上,则n的值= . 15. 如图,点A , B分别在函数图象的两支上(在第一象限),连接交轴于点 . 点D , E在函数图象上,轴,轴,连接DE , BE . 若 , 的面积为9,四边形ABDE的面积为14,则的值为 .
15. 如图,点A , B分别在函数图象的两支上(在第一象限),连接交轴于点 . 点D , E在函数图象上,轴,轴,连接DE , BE . 若 , 的面积为9,四边形ABDE的面积为14,则的值为 .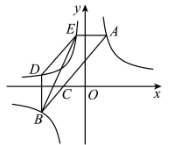
三、解答题
-
16. 如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数的函数交于A(-2,b),B两点.
 (1)、求一次函数的表达式;(2)、在x轴上是否存在点C,使△ABC的周长最小,若存在,求出点C的坐标,若不存在,请说明理由.17. 已知反比例函数的图象经过第一、三象限.(1)、求的取值范围;(2)、若 , 此函数的图象过第一象限的两点 , , 且 , 求的取值范围.18. 如图,在平面直角坐标系中,O为坐标原点,的边垂直于x轴,垂足为点B , 反比例函数的图象经过的中点C , 交于点D.若点D的坐标为 , 且.
(1)、求一次函数的表达式;(2)、在x轴上是否存在点C,使△ABC的周长最小,若存在,求出点C的坐标,若不存在,请说明理由.17. 已知反比例函数的图象经过第一、三象限.(1)、求的取值范围;(2)、若 , 此函数的图象过第一象限的两点 , , 且 , 求的取值范围.18. 如图,在平面直角坐标系中,O为坐标原点,的边垂直于x轴,垂足为点B , 反比例函数的图象经过的中点C , 交于点D.若点D的坐标为 , 且. (1)、求反比例函数的表达式;(2)、设点E是线段上的动点(不与点C、D重合),过点E且平行y轴的直线与反比例函数的图象交于点F , 求面积的最大值.
(1)、求反比例函数的表达式;(2)、设点E是线段上的动点(不与点C、D重合),过点E且平行y轴的直线与反比例函数的图象交于点F , 求面积的最大值.