【培优卷】2024年浙教版数学八年级下册3.2 中位数和众数
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（ ）A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大2. 5名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（ ）A、40% B、56% C、60% D、62%3. 某班体育委员统计了全班名同学一周的体育锻炼时间（单位：）并绘制了如图所示的折线统计图，下列说法：众数是；中位数是；平均数是；锻炼时间不低于的人数有人，其中正确的是（ ）
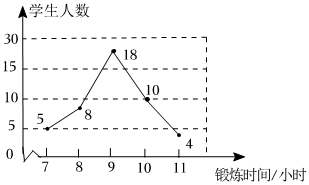A、 B、 C、 D、4. 某班七个兴趣小组人数分别为4，4，5，5，x，6，7，已知这组数据的平均数是5，则这组数据的中位数和众数分别是（ ）A、5，5 B、5，4 C、4，4 D、4，55. 某中学举办了以“放歌新时代奋进新征程”为主题的知识竞答比赛（共10道题，每题1分）．已知选取了10名学生的成绩，且10名学生成绩的中位数和众数相同，但在记录时遗漏了一名学生的成绩．如图是参赛9名学生的成绩，则这10名学生成绩的中位数是（ ）
A、7 B、7.5 C、8 D、9二、填空题
-
6. 已知一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数为.7. 一组数据为1，3，5，12，a，其中整数a是这组数据的中位数，则该组数据的平均数是.8. 两组数据： ， ， ， 与 ， ， 的平均数都是 ， 若将这两组数据合并为一组新数据： ， ， ， ， ， ， ， 则这组新数据的众数为 ．9. 已知一组数据23，25，20，15，x，15，若它们的中位数是21，那么它们的平均数为。
三、综合题
-
10. 已知一组数据：x，10，12，6的中位数与平均数相等，求x的值。11. 年新春伊始，中国电影行业迎来了期盼已久的火爆场面，满江红、流浪地球、无名、深海等一大批电影受到广大影迷的青睐如图的统计图是其中两部电影上映后前六天的单日票房信息根据以上信息，回答下列问题：
(1)、1月日日的六天时间内，影片甲单日票房的中位数为 亿元；(2)、求月日日的六天时间内影片乙的平均日票房精确到亿元；(3)、对于甲、乙两部影片上映前六天的单日票房，下列说法中所有正确结论的序号是 ．影片甲的单日票房逐日增加；
影片乙的单日票房逐日减少；
通过前六天的数据比较，甲单日票房的方差小于乙单日票房的方差；
在前六天的单日票房统计中，甲单日票房和乙单日票房之间的差值在月日达到最大．
12. 为了解我国2022年25个地区第一季度快递业务收入情况，收集了这25个地区第一季度快递业务收入（单位：亿元）的数据，并对数据进行了整理、描述和分析，给出如下信息．
a．排在前5位的地区第一季度快递业务收入的数据分别为：
5349 437.0 270.3 187.7 104.0b．其余20个地区第一季度快递业务收入的数据的频数分布表如下：
快递业务收入x
频数
6
10
1
3
c．第一季度快递业务收入的数据在这一组的是：
20.2 20.4 22.4 24.2 26.1 26.5 28.5 34.4 39.1 39.8d．排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下：
前5位的地区
其余20个地区
全部25个地区
平均数
306.8
29.9
n
中位数
270.3
m
28.5
根据以上信息，回答下列问题：
(1)、表中m的值为；(2)、在下面3个数中，与表中n的值最接近的是（填写序号）；①30 ②85 ③150
(3)、根据（2）中的数据，预计这25个地区2022年全年快递业务收入约为亿元．13. 为培养学生良好的运动习惯，提高学生的身体素质，我校开展了“花样跳绳”和“春季长跑”等体育活动.体育老师随机抽取了八年级男、女各60名学生的长跑成绩，并将数据进行整理分析，给出了下面部分信息：数据分为A，B，C，D四个等级，分别是：
A： ， B： ， C： ， D：
60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：
男生成绩位于B等级前10名的分数为：
95，95，95，94，94，94，92，91，90，90.
60名男生和60名女生成绩的平均数，中位数，众数如下表：
性别
平均数
中位数
众数
男生
94
a
96
女生
95
94
96
根据以上信息，解答下列问题：
(1)、填空： ， ；(2)、计算抽取的男生成绩在B等级的人数，并补全条形统计图；(3)、根据以上数据，你认为在此次活动中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）．(4)、若该年级有800名学生，估计成绩为A等级的学生约为人．14. 某市语委办为了解本市八年级学生汉字书写能力情况，随机抽查了部分八年级学生，并将调查数据进行整理，请解答以下问题：正确书写出的字数x（个）
频数（人）
频率
0≤x≤5
8
0.16
5＜x≤10
10＜x≤15
16
0.32
15＜x≤20
8
0.16
20＜x≤25
4
0.08
25＜x≤30
2
0.04
(1)、把频数、频率分布表和频数分布直方图补充完整；(2)、根据统计图，可知“正确书写的字数”的中位数应处的范围是 ；(3)、若正确书写的字数不超过15个为不及格，请求出不及格人数占所抽查人数的百分比；并根据调查数据估计，该市20000名八年级学生中，有多少名学生不及格？对此，请你用一句话谈谈你的建议或感想．15. 为了让师生更规范地操作教室里的一体机设备，学校信息技术处制作了“教室一体机设备培训”视频，并在读报课时间进行播放．结束后为了解初中校部、高中校部各班一体机管理员对设备操作知识的掌握程度，得分用x（x为整数）表示，A：60≤x＜70，B：70≤x＜80，C：80≤x＜90，D：90≤x≤100，对得分进行整理分析，给出了下面部分信息：初中一体机管理员的测试成绩在C组中的数据为：81，85，88．
高中一体机管理员的测试成绩：76，83，71，100，81，100，82，88，95，90，100，86，89， 93，86．
成绩统计表如下：
学部
平均数
中位数
众数
初中
88
a
98
高中
88
88
b
(1)、a＝ ， b＝ ．(2)、通过以上数据分析．你认为 ▲ （填“初中”或“高中”）的一体机管理员对一体机设备操作的知识掌握的更好，请写出理由；(3)、若初中校部有100名一体机管理员，高中校部有140名一体机管理员，请估计此次浏试成绩达到90分及以上的一体机管理员共有多少人？16. 某县教育局为了对该区八年级数学学科教学质量进行检查，对该区八年级的学生进行摸底，为了解摸底的情况，进行了抽样调查，过程如下，请将有关问题补充完整．收集数据：随机抽取 学校与 学校的各20名学生的数学成绩（单位：分）进行分析：
学校
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
学校
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
(1)、整理、描述数据：按如下数据段整理、描述这两组数据分段
学校
30≤x≤39
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
学校
1
1
0
0
3
7
8
学校
(2)、分析数据：两组数据的平均数、中位数、众数、方差如下表：统计量
学校
平均数
中位数
众数
方差
学校
81.85
88
91
268.43
学校
81.95
86
m
115.25
(3)、得出结论：：若 学校有800名八年级学生，估计这次考试成绩80分以上（包含80分）人数为多少人?
：根据表格中的数据，推断出哪所学校学生的数学水平较高，并说明理由．（至少从两个不同的角度说明推断的合理性）
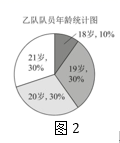
17. 甲、乙两支运动队各有10名队员，他们的年龄分布情况分别如图、表所示：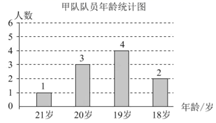
甲、乙两队队员年龄统计表
平均数（近似值）
众数
中位数
甲队
a
①
②
乙队
20
③
b
解决下列问题：
(1)、求甲队队员的平均年龄a的值．（结果取整数）(2)、补全统计表中的①②③三处．(3)、阅读理解-----扇形图中求中位数的方法．[阅读与思考]
小明同学在求乙队队员年龄的中位数b时，是这样思考的：因为中位数是将一组数据按大小排序后，排在中间位置的一个数或中间两个数的平均数，那就需要先找到数据按大小排序后，大致排在50%附近的数，再根据中位数的概念进行细化求解．
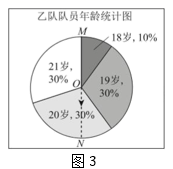
图2这个扇形图中的数据18~21是按大小顺序旋转排列的，我们就可以像图3所示的这样，先找到最大数据“21”与最小数据“18”的分界半径OM，为找到排在50%附近的数，再作出直径MN，那么射线ON指向的数据就是中位数．
王老师的评价：小明的这个方法是从中位数的概念出发，充分利用了扇形图的特性形象直观地解决问题．
[理解与应用]
请你利用小明的方法直接写出统计表中b的值．
