【提升卷】2024年浙教版数学八年级下册3.1 平均数

试卷更新日期：2024-01-20 类型：同步测试

进入出卷网下载

一、选择题

1. 在“双减”政策下，某学校规定，学生的学期学业成绩由两部分组成：平时成绩占40%，期末成绩占60%，小颖的平时、期末成绩分别为80分，90分，则小颖本学期的学业成绩为（）

A、92分 B、90分 C、86分 D、85分

查看试题解析
2. 在一次献爱心的捐款活动中，某班50名同学的捐款金额如图所示，则在这次捐款活动中，该班同学捐款金额的平均数是（）

A、14.2元 B、15元 C、16.2元 D、20.25元

查看试题解析
3. 在凤凰山教育共同体数学学科节中，为展现数学的魅力，M老师组织了一个数学沉浸式互动游戏：随机请A ， B ， C ， D ， E五位同学依次围成一个圆圈，每个人心里先想好一个实数，并把这个数悄悄的告诉相邻的两个人，然后每个人把与自己相邻的两个人告诉自己的数的平均数报出来．若A ， B ， C ， D ， E五位同学报出来的数恰好分别是1，2，3，4，5，则D同学心里想的那个数是（）

A、 $- 3$ B、 $- 4$ C、5 D、9

查看试题解析
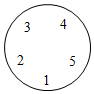4. 某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元，某天的销售情况如图所示，则这天销售矿泉水的平均单价是（）

A、1.95元 B、2.15元 C、2.25 元 D、2.75 元

查看试题解析
5. 已知数据x₁，x₂，⋯，x_n的平均数是2，则 3x₁-2，3x₂-2，…，3x，-2的平均数是（）

A、0 B、2 C、4 D、6

查看试题解析

二、填空题

6. 若数2，3，x，5，6五个数的平均数为4，则x的值为．

查看试题解析
7. 小刚开学后，第一次测试数学得了70分，语文得了84分，则英语至少得分，才能使三科平均分不低于80分．

查看试题解析

8. 为提高学生对个人健康的重视，某班级举办“七步洗手法”比赛活动，小明的单项成绩如下表所示（各项成绩均按百分制计）：

项目	书面测试	实际操作	宣传展示
成绩（分）	96	98	96

若按书面测试占30%、实际操作占50%、宣传展示占20%，计算参赛个人的综合成绩（百分制），则小明的最后得分是．

查看试题解析

9. 已知某校女子田径队23人年龄的平均数是13岁，但是后来发现其中一位同学的年龄登记出现错误，将14岁写成了15岁，经重新计算后，正确的平均数为a岁，则a13（在横线上填上“＞”或“＝”或“＜”）．

查看试题解析
10. 设一个样本数据为 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， … $x_{n}$ ，它的平均数为5，则另一个样本数据 $3 x_{1} - 5$ ， $3 x_{2} - 5$ ， … $3 x_{n} - 5$ 的平均数是．

查看试题解析
11. 一组数据：4，6，12分别以 $\frac{1}{4}$ ， $\frac{1}{3}$ ， $\frac{5}{12}$ 为权的加权平均数为．

查看试题解析

三、解答题

12. 学校团委组织了一次“中国梦 $\cdot$ 航天情”系列活动．下面是八年级甲，乙两个班各项目的成绩（单位：分） $：$
项目
班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87

(1)、如果根据三项成绩的平均分计算最后成绩，请通过计算说明甲、乙两班谁将获胜；

(2)、如果将知识竞赛、演讲比赛、版面创作按 $5 ： 3 ： 2$ 的比例确定最后成绩，请通过计算说明甲乙两班谁将获胜．

查看试题解析

13. 某市招聘教师，采取的是“笔试+专业测试”的形式，笔试成绩和专业测试成绩按

6 ： 4

合成报考人员的综合成绩，最终录用则依据招聘计划按综合成绩从高到低确定．

	教学设计	课堂教学	答辩
甲	90	85	90
乙	80	92	85

（注：每组含最小值，不含最大值）

(1)、将笔试入围的报考人员的成绩绘制成如图所示的频数分布直方图，其中成绩80分以上（包括80分）的人数占40%，则笔试入围的共有多少人？补全频数分布直方图；

(2)、专业测试包括教学设计、课堂教学、答辩三项测试，已知甲、乙两人的笔试成绩分别为80分，82分，在笔试入围后，参加了专业测试，两人的成绩如表格所示：（单位：分）根据招聘公告规定，专业测试成绩按教学设计占30%、课堂教学占50%、答辩占20%来计算，若按综合成绩在甲、乙两人中录用一人，谁将被录用？

查看试题解析

14. 阳阳八年级下学期的数学成绩如下表所示：
测验类别
平时测验1
平时测验2
平时测验3
平时测验4
期中考试
期末考试
成绩（分）
108
104
116
112
112
110

(1)、阳阳该学期的数学平时测验的平均成绩分；

(2)、如果学期的综合成绩是根据如图所示的权重计算，请计算出阳阳该学期的数学综合成绩．

查看试题解析
15. 某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位： $m^{2}$ ）和材积量（单位： $m^{3}$ ），得到如下数据：
样本号
1
2
3
4
5
6
7
8
9
10
根部横截面积x
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
材积量y
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40

(1)、估计该林区一颗这种树木平均根部横截面积与平均材积量．

(2)、现测量了该林区部分这种树木的根部横截面积，经过测算得到这种树木的根部横截面积总和为 $2000 m^{2}$ ．已知树木的材积量与其根部横截面积近似成正比．利用以上数据估计该林区这种树木的总材积量．

查看试题解析

测验类别	平时测验1	平时测验2	平时测验3	平时测验4	期中考试	期末考试
成绩（分）	108	104	116	112	112	110

样本号	1	2	3	4	5	6	7	8	9	10
根部横截面积x	0.04	0.06	0.04	0.08	0.08	0.05	0.05	0.07	0.07	0.06
材积量y	0.25	0.40	0.22	0.54	0.51	0.34	0.36	0.46	0.42	0.40