山东省昌乐重点中学2024届高三上学期数学1月模拟预测试卷

试卷更新日期：2024-01-20 类型：高考模拟

进入出卷网下载

一、选择题：(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)

1. 已知复数 $z_{i} ， z_{2}$ 在复平面内对应的点分别为 $Z_{1} (1 ， 1) ， Z_{2} (0 ， 1) ，则 \frac{z_{1}}{z_{2}}$ 的虚部为（）

A、1 B、 $- i$ C、 $i$ D、 $- 1$

查看试题解析
2. 设 $a \in R$ ，则“ $s i n α = c o s α$ ”是“ $α = \frac{π}{4}$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 若正数 $a ， b$ 满足 $a b = a + b + 3$ ，则 $a + b$ 的取值范围是（）

A、 $[6 ， + \infty)$ B、 $[9 ， + \infty)$ C、（0，6] 　 D、（0，9）

查看试题解析
4. 具有线性相关关系的变量 $x ， y$ 的一组数据如下：
x
0
1
2
3
y
-5
-4.5
-4.2
-3.5
其线性回归直线方程为 $\hat{y} = \hat{b} x + \hat{a}$ ，则回归直线经过（）

A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限

查看试题解析
5. 已知点 $M (2 ， 4)$ 在抛物线C： $y^{2} = 2 p x$ ( $p > 0$ )上，点M到抛物线C的焦点的距离是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 在 $Δ A B C$ 中， $\overset{\leftrightarrow}{A B} + \overset{\leftrightarrow}{A C} = 2 \overset{\leftrightarrow}{A D}$ ， $\overset{\leftrightarrow}{A E} + 2 \overset{\leftrightarrow}{D E} = \overset{\leftrightarrow}{0}$ ，若 $\overset{\leftrightarrow}{E B} = x \overset{\leftrightarrow}{A B} + y \overset{\leftrightarrow}{A C}$ ，则（）

A、 $y = 2 x$ B、 $y = - 2 x$ C、 $x = 2 y$ D、 $x = - 2 y$

查看试题解析
7. 已知奇函数 $f (x)$ 是 $R$ 上增函数， $g (x) = x f (x)$ ，则（）

A、 $g (l o g_{3} \frac{1}{4}) > g (2^{- \frac{3}{2}}) > g (2^{- \frac{2}{3}})$ B、 $g (l o g_{3} \frac{1}{4}) > g (2^{- \frac{2}{3}}) > g (2^{- \frac{3}{2}})$ C、 $g (2^{- \frac{3}{2}}) > g (2^{- \frac{2}{3}}) > g (l o g_{3} \frac{1}{4})$ D、 $g (2^{- \frac{2}{3}}) > g (2^{- \frac{3}{2}}) > g (l o g_{3} \frac{1}{4})$

查看试题解析
8. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 ， (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2} ， O$ 为坐标原点，P是双曲线在第一象限上的点， $\vec{| P F_{1} |} = 2 \vec{| P F_{2} |} = 2 m ， (m > 0) ， \vec{P F_{1}} \cdot \vec{P F_{2}} = m^{2}$ ，则双曲线C的渐近线方程为（）

A、 $y = \pm \frac{1}{2} x$ B、 $y = \pm \frac{\sqrt{2}}{2} x$ C、 $y = \pm x$ D、 $y = \pm \sqrt{2} x$

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项是符合题目要求，全部选对的得5分，部分选对的得3分，有选错的0分.

9. 下列命题中的真命题是（）

A、 $\forall x \in R ， 2^{x - 1} > 0$ B、 $\forall x \in N^{*} ， {(x - 1)}^{2} > 0$ C、 $\exists x_{0} \in R ， 1 g x_{0} < 1$ D、 $\exists x_{0} \in R ， t a n x_{0} = 2$

查看试题解析
10. 将函数 $f (x) = \sin 2 x$ 的图象向右平移 $\frac{π}{4}$ 个单位后得到函数 $g (x)$ 的图象，则函数 $g (x)$ 具有性质（）

A、在 $(0 ， \frac{π}{4})$ 上单调递增，为偶函数 B、最大值为1，图象关于直线 $x = - \frac{3 π}{2}$ 对称 C、在 $(- \frac{3 π}{8} ， \frac{π}{8})$ 上单调递增，为奇函数 D、周期为 $π$ ，图象关于点 $(\frac{3 π}{4} ， 0)$ 对称

查看试题解析
11. 已知 $m 、 n$ 为两条不重合的直线， $α 、 β$ 为两个不重合的平面，则下列说法正确的是（）

A、若 $m//α ， n//β$ 且 $α//β ，$ 则 $m//n$ B、若 $m//n ， m ⊥ α ， n ⊥ β ，$ 则 $α//β$ C、若 $m//n ， n \subset α ， α//β ， m ⊄ β ，$ 则 $m//β$ D、若 $m//n ， n ⊥ α ， α ⊥ β ，$ 则 $m//β$

查看试题解析
12. 设等比数列 ${a_{n}}$ 的公比为q，其前n项和为 $S_{n}$ ，前n项积为 $T_{n}$ ，并满足条件 $a_{1} > 1 ， a_{2019} a_{2020} > 1$ ， $\frac{a_{2019} - 1}{a_{2020} - 1} < 0$ ，下列结论正确的是（）

A、 $S_{2019}^{} < S_{2020}^{}$ B、 $a_{2019}^{} a_{2021}^{} - 1 < 0$ C、 $T_{2019}^{}$ 是数列 ${T_{n}}$ 中的最大值 D、数列 ${T_{n}}$ 无最大值

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

13. 已知直线 $x - y + a = 0$ 与圆 $x_{}^{2} + y_{}^{2} = 2$ 相交于 $A ， B$ 两点( $O$ 为坐标原点)，且 $Δ A O B$ 为等腰直角三角形，则实数 $a$ 的值为.

查看试题解析
14. 已知直线 $y = x + 2$ 与曲线 $y = l n (x + a)$ 相切，则 $a$ 的值为.

查看试题解析
15. 2019年7月，中国良渚古城遗址获准列入世界遗产名录，标志着中华五千年文明史得到国际社会认可．良渚古城遗址是人类早期城市文明的范例，实证了中华五千年文明史．考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律．已知样本中碳14的质量N随时间T(单位：年)的衰变规律满足 $N = N_{0} \cdot 2^{\frac{- T}{5730}}$ ( $N_{0}$ 表示碳14原有的质量)，则经过5730年后，碳14的质量变为原来的；经过测定，良渚古城遗址文物样本中碳14的质量是原来的 $\frac{3}{7} 至 \frac{1}{2}$ ，据此推测良渚古城存在的时期距今约在5730年到年之间．(参考数据：lg2≈0.3，lg7≈0.84，lg3≈0.48)

查看试题解析
16. 已知四面体 $A B C D$ 中， $A B = A D = B C = D C = B D = 5 ， A C = 8$ ，则四面体 $A B C D$ 的体积为

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 在 $Δ A B C$ ， a ， b ， c分别为内角A ， B ， C的对边，且 $8 a b s i n C = 3 (b^{2} + c^{2} - a^{2})$ ，若 $a = \sqrt{10}$ ， $c = 5$ .

(1)、求 $c o s A$ ；

(2)、求 $Δ A B C$ 的面积S.

查看试题解析
18. 设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $a_{1} = 1 ， S_{n + 1} - 2 S_{n} = 1 ， n \in N^{*}$ ．

(1)、证明： ${S_{n} + 1}$ 为等比数列，求出 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = \frac{n}{a_{n}}$ ，求 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
19. 如图所示的多面体中，底面ABCD为矩形， $B E ⊥$ 平面ABCD ， $C C_{1} ⊥$ 平面ABCD ， $D F ⊥$ 平面ABCD ， $A F / / E C_{1}$ ，且AB=4，BC=2， $C C_{1} = 3$ ， BE=1．

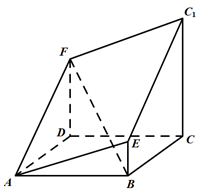(1)、求BF的长；

(2)、求直线 $C C_{1}$ 与平面 $A E C_{1} F$ 成的角的正弦值．

查看试题解析
20. 2018年非洲猪瘟在东北三省出现，为了防控，某地生物医药公司派出技术人员对当地甲、乙两个养殖场提供技术服务，两种方案如下：
方案一：公司每天收取养殖场技术服务费40元，对于需要用药的每头猪收取药费2元，不需要用药的不收费；
方案二：公司每天收取养殖场技术服务费120元，若需要用药的猪不超过45头，不另外收费，若需要用药的猪超过45头，超过的部分每头猪收费标准为8元.

(1)、设日收费为 $y$ （单位：元），每天需要用药的猪的数量为 $n$ （单位：头），试写出两种方案中 $y$ 与 $n$ 的函数关系式；

(2)、若该生物医药公司从10月1日起对甲养殖场提供技术服务，10月31日该养殖场对其中一个猪舍9月份和10月份的猪的发病数量（单位：头）进行了统计，得到了如下的列联表：

9月份
10月份
合计
未发病
40
85
125
发病
65
20
85
合计
105
105
210
根据以上列联表判断是否有 $99.9 %$ 的把握认为猪未发病与该生物医药公司提供技术服务有关.
附：
$P (K^{2} \geq k_{0})$
0.050
0.010
0.001
$k_{0}$
3.841
6.635
10.828

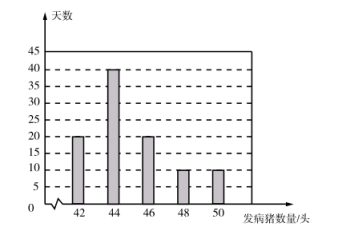
(3)、当地的丙养殖场对过去100天的猪的发病情况进行了统计，得到如图所示的条形图.依据该统计数据，把频率视为概率，从节约养殖成本的角度去考虑，若丙养殖场计划结合以往经验，从两个方案中选择一个，那么选择哪个方案更合适，请说明理由.

查看试题解析
21. 已知函数 $f (x) = l n x - a + \frac{a}{x} (a > 0)$ ．

(1)、若曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处与 $x$ 轴相切，求 $a$ 的值；

(2)、求函数 $f (x)$ 在区间 $(1 ， e)$ 上的零点个数．

查看试题解析
22. 给定椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，称圆心在原点 $O$ ，半径为 $\sqrt{a^{2} + b^{2}}$ 的圆是椭圆C的“卫星圆”.若椭圆C的离心率 $\frac{\sqrt{2}}{2}$ ，点 $(2 ， \sqrt{2})$ 在C上．

(1)、求椭圆C的方程和其“卫星圆”方程；

(2)、点P是椭圆C的“卫星圆”上的一个动点，过点P作直线 $l_{1} ， l_{2} ，$ 使其与椭圆C都只有一个交点，且 $l_{1}^{} ， l_{2}^{}$ 分别交其“卫星圆”于点M，N，证明：弦长 $| M N |$ 为定值．

查看试题解析

	9月份	10月份	合计
未发病	40	85	125
发病	65	20	85
合计	105	105	210

$P (K^{2} \geq k_{0})$	0.050	0.010	0.001
$k_{0}$	3.841	6.635	10.828

x	0	1	2	3
y	-5	-4.5	-4.2	-3.5