重庆市渝北区松树桥名校2023-2024学年高一上学期数学第三次诊断试卷
试卷更新日期:2024-01-20 类型:月考试卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列各角,与330°角的终边相同的角是( )A、510° B、150° C、-150° D、-390°2. 设 , , 则( )A、 B、 C、 D、3. 下列函数中,既是奇函数又是增函数的是( )A、 B、 C、 D、4. 若 , 则的大小关系为( )A、 B、 C、 D、5. 已知 , 则=( )A、 B、 C、或1 D、或16. 已知 , , , 则的最小值为( )A、8 B、13 C、12 D、97. 若定义在R的偶函数在上单调递增,且 , 则满足的x的取值范围是( )A、 B、 C、 D、8. 函数的部分图象大致为( )A、
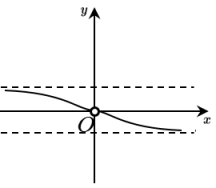 B、
B、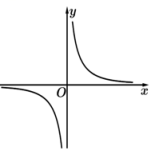 C、
C、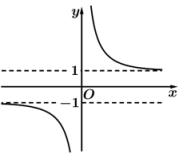 D、
D、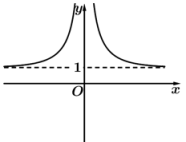
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 下列说法中,正确的是( )A、是第二象限角 B、第三象限角大于第一象限角 C、若角为第三象限角,那么为第二象限角 D、若角与角的终边在一条直线上,则10. 下列命题中是真命题的是( )A、已知 , 则的值为11 B、若 , 则函数的最小值为 C、函数是偶函数 D、函数在区间内必有零点11. 下列说法正确的是( )A、“”的否定为“” B、函数的单调递增区间是 C、已知扇形的面积是 , 半径是 , 则扇形的圆心角的弧度数为4 D、已知函数的定义域为 , 则函数的定义域为12. 已知函数 , 则下列选项正确的是( )A、函数的值域为 B、方程有两个不等的实数解 C、不等式的解集为 D、关于的方程的解的个数可能为
三、填空题:本大题4个小题,每小题5分,共20分.各题答案必须填写在答题卡上相应位置(只填结果,不写过程).
-
13. 已知函数(且)的图象恒过定点 , 则点的坐标为.14. 已知函数在上有一个零点,用二分法求零点的近似值(精确度为0.1时,至少需要进行次函数值的计算.15. 函数 , 的值域是 .16. 已知 , 且为第四象限角,则 .
四、解答题:本大题6个小题,共70分.各题解答必须答在答题卡上(必须写出必要的文字说明、演算步骤或推理过程).
-
17. 设函数的定义域为 , 集合().(1)、求集合;(2)、若: , : , 且是的必要不充分条件,求实数的取值范围.18. 已知的最小正周期为π.(1)、求ω的值;(2)、求的单调递增区间;(3)、求在区间上的最大值.19. 已知角以x轴的非负半轴为始边,为终边上一点.(1)、求的值;(2)、求的值.20. 已知点在幂函数的图象上,.(1)、求的解析式;(2)、若 , 且方程有解,求实数的取值范围;(3)、当时,解关于的不等式.21. 华为为了进一步增加市场竞争力,计划在2023年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本250万,每生产(千部)手机,需另投入成本万元,且 , 由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完(1)、求出2023年的利润(万元)关于年产量(千部)的函数解析式(利润=销售额-成本)(2)、2023年产量为多少(千部)时,企业所获利润最大?最大利润是多少?22. 已知函数.(1)、当时,求关于的不等式的解集;(2)、 , 关于的方程在总有两个不同实数解,求实数的取值范围;(3)、若在区间上恒成立,求实数的取值范围.