上海市嘉定区重点中学2023-2024学年高二上学期数学12月月考试卷

试卷更新日期：2024-01-20 类型：月考试卷

进入出卷网下载

一、填空题（本大题共54分，1-6每题4分；7-12每题5分）

1. 已知向量 $\vec{a} = (1 ， 2 ， - 2)$ 与 $\vec{b} = (m ， m - 2 ， 1)$ 垂直，则m的值为.

查看试题解析
2. 计算： $\sum_{i = 1}^{+ \infty} {(\frac{1}{3})}^{i - 1} =$ .

查看试题解析
3. 已知圆锥的轴截面是一个顶角为 $\frac{2 π}{3}$ ，腰长为2的等腰三角形，则该圆锥的体积为.

查看试题解析
4. 如图，以长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的顶点 $D$ 为坐标原点，过 $D$ 的三条棱所在的直线为坐标轴，建立空间直角坐标系，若 $\overset{⇀}{D B_{1}}$ 的坐标为 $(4 ， 3 ， 2)$ ，则 $\overset{⇀}{A C_{1}}$ 的坐标为

查看试题解析
5. 将一段长12 $c m$ 的铁丝折成两两互相垂直的三段，使三段长分别为3 $c m$ ､4 $c m$ ､5 $c m$ ，则原铁丝的两个端点之间的距离为 $c m$ .

查看试题解析
6. 一个圆锥的侧面展开图是一个半径为 $R$ 的半圆，则这个圆锥的底面积是.

查看试题解析
7. 从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为．

查看试题解析
8. 如图所示， $△ A^{'} B^{'} O^{'}$ 是利用斜二测画法画出的 $△ A B O$ 的直观图，已知 $A' B' / / y^{'}$ 轴， $O^{'} B^{'} = 4$ ，且 $△ A B O$ 的面积为16，过 $A ′$ 作 $A^{'} C^{'} ⊥ x^{'}$ 轴，则 $A^{'} C^{'}$ 的长为.

查看试题解析
9. 已知 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和， $S_{n} + 1 = S_{n - 1} + a_{n - 1} (n \geq 2 ， n \in N^{*})$ 且 $S_{8} = 4 S_{4}$ ，则 $a_{11} =$ ．

查看试题解析
10. 在《九章算术》第五卷《商功》中，将底面为正方形，顶点在底面上的射影为底面中心的四棱锥称为方锥，也就是正四棱锥.已知球 $O$ 内接方锥 $P - A B C D$ 的底面 $A B C D$ 过球心 $O$ ，若方锥 $P - A B C D$ 的体积为 $\frac{2}{3}$ ，则球 $O$ 的表面积为。

查看试题解析
11. 已知平面 $α$ 的法向量为 $\vec{n} = (- 2 ， - 2 ， 1)$ ，点 $A (x ， 3 ， 0)$ 在平面 $α$ 内，若点 $P (- 2 ， 1 ， 4)$ 到平面 $α$ 的距离 $d$ 为 $\frac{10}{3}$ ，则 $x =$ .

查看试题解析
12. 若正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为3，P是正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 表面上一动点.设 $Ω$ 是以P为球心，半径为1的动球在运动过程中经过区域的全体，则 $Ω$ 的体积为.

查看试题解析

二、选择题（本大题共18分，13-14每题4分，15-16每题5分）

13. 下列结论：①如果 $P (A) = 0.9999$ ，那么 $A$ 为必然事件：
②若事件 $A$ 与 $B$ 是互斥事件，则 $P (A) + P (B) = 1$ ；
③概率是随机的，试验前不能确定；
④若事件 $A$ 与 $B$ 是对立事件，则 $A$ 与 $B$ 一定是互斥事件．
其中是正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
14. 下列说法不正确的是（）

A、空间中，一组对边平行且相等的四边形是一定是平行四边形； B、同一平面的两条垂线一定共面； C、过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内； D、过一条直线有且只有一个平面与已知平面垂直.

查看试题解析
15. 如图是正方体的平面展开图，在这个正方体中，①BM与ED平行；②CN与BE是异面直线；③CN与BM成60°；④DM与BN垂直.以上四个命题中，正确命题的序号是（）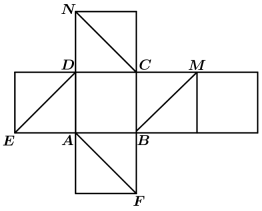

A、①②③ B、②④ C、③④ D、②③④

查看试题解析
16. 如图，已知正四面体 $A_{1} A_{2} A_{3} A_{4}$ ，点 $A_{5}$ ， $A_{6}$ ， $A_{7}$ ， $A_{8}$ ， $A_{9}$ ， $A_{10}$ 分别是所在棱中点，点 $P$ 满足 $\vec{A_{4} P} = x \vec{A_{4} A_{1}} + y \vec{A_{4} A_{2}} + z \vec{A_{4} A_{3}}$ 且 $x + y + z = 1$ ，记 $| \vec{A_{4} Q} | = | \vec{A_{4} P} |_{m i n}$ ，则当 $1 \leq i$ ， $j \leq 10$ 且 $i \neq j$ 时，数量积 $\vec{A_{4} Q} \cdot \vec{A_{i} A_{j}}$ 的不同取值的个数是（）

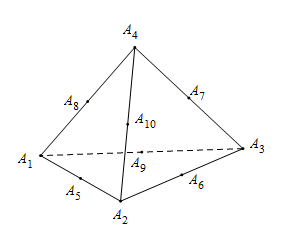A、3 B、5 C、9 D、21

查看试题解析

三、解答题（本大题共有5题，满分78分）．

17. 公差不为零的等差数列 ${a_{n}}$ 中， $a_{1} ， a_{2} ， a_{5}$ 成等比数列，且该数列的前10项和为100．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = a_{n} - 10$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ 的最小值．

查看试题解析
18. 如图，在正三棱柱 $B C D - B_{1} C_{1} D_{1}$ 与四棱锥 $A - B D D_{1} B_{1}$ 组成的组合体中，底面 $A B C D$ 恰好是边长为2菱形，且 $C C_{1} = 2$ ．

(1)、求证： $A D_{1} / /$ 平面 $B C C_{1} B_{1}$

(2)、设E是 $B D$ 的中点，求直线 $B_{1} E$ 与直线 $A D_{1}$ 所成角的余弦值．

查看试题解析
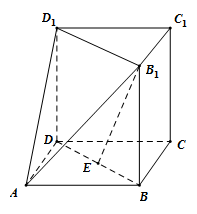19. 已知正方形ABED的边长为 $\sqrt{2}$ ， O为两条对角线的交点，如图所示，将 $R t △ B E D$ 沿BD所在的直线折起，使得点E移至点C ，满足 $A B = A C$ ．

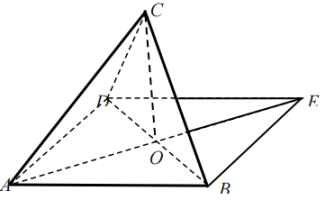(1)、求四面体ABCD的体积V；

(2)、求直线BC与平面ACD所成的角的大小．

查看试题解析
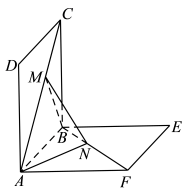20. 如图，正方形 $A B C D$ 、 $A B E F$ 的边长都是1，而且平面 $A B C D$ 、 $A B E F$ 互相垂直．点M在 $A C$ 上移动，点N在 $B F$ 上移动，若 $C M = B N = a (0 < a < \sqrt{2})$ ．

(1)、求 $M N$ 的长；

(2)、a为何值时， $M N$ 的长最小；

(3)、当 $M N$ 的长最小时，求面 $M N A$ 与面 $M N B$ 所成二面角 $α$ 的大小．

查看试题解析

21. 某公司实行了年薪制工资结构改革．该公司从2023年起，每人的工资由三个项目构成，并按下表规定实施：

项目	金额[万元（人·年）]	性质与计算方法
基础工资	2022年基础工资的1万元	考虑到物价因素，决定从2023年起每年递增 $10 %$ （年入职年限无关，2023年基本工资的 $1$ 万元）
房屋补贴	008万元	从2023年起，按职工到公司年限计算，每年递增008万元
医疗费	0.32万元	固定不变

如果该公司2023年有5位职工，计划从2024年起每年新招5名职工．若2023年算第一年

(1)、求第三年公司付给职工的工资总额.

(2)、将第

n

年该公司付给职工工资总额

y

（万元）表示成年限

n

的函数；

(3)、若公司每年发给职工工资总额中，房屋补贴和医疗费之和总是不会超过基础工资总额的

P %

，求

P

的最小值．

查看试题解析