北京市八一重点学校2023-2024学年高二上学期数学12月月考试卷
试卷更新日期:2024-01-20 类型:月考试卷
一、选择题:本大题共10小题,每题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.
-
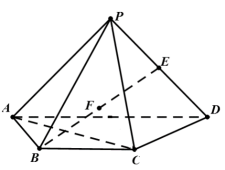
1. 已知椭圆 上的点 到椭圆一个焦点的距离为7,则 到另一焦点的距离为( )A、2 B、3 C、5 D、72. 已知是平面内两个不同的定点,为平面内的动点,则“的值为定值 , 且”是“点的轨迹是双曲线”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 直线与圆的公共点个数为( )A、个 B、个 C、个 D、个或个4. 在四面体 中,点 为棱 的中点. 设 , , ,那么向量 用基底 可表示为( )
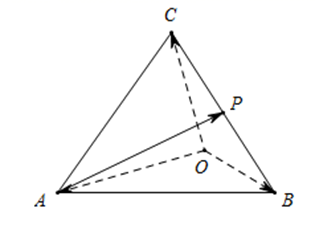 A、 B、 C、 D、5. 已知点 , 若线段的垂直平分线的方程是 , 则实数的值是( )A、 B、 C、3 D、16. 如图,在正三棱柱中, , 则与平面所成角的余弦值为( )
A、 B、 C、 D、5. 已知点 , 若线段的垂直平分线的方程是 , 则实数的值是( )A、 B、 C、3 D、16. 如图,在正三棱柱中, , 则与平面所成角的余弦值为( )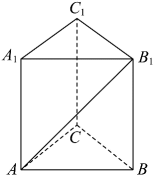 A、 B、 C、 D、7. 已知F为椭圆C: =1(a>b>0)的右焦点,O为坐标原点,P为椭圆C上一点,若|OP|=|OF|,∠POF=120°,则椭圆C的离心率为( )A、 B、 C、 -1 D、 -18. 如图,正方体的棱长为4,动点 , 在棱上,且 , 动点在棱上,则三棱锥的体积( )
A、 B、 C、 D、7. 已知F为椭圆C: =1(a>b>0)的右焦点,O为坐标原点,P为椭圆C上一点,若|OP|=|OF|,∠POF=120°,则椭圆C的离心率为( )A、 B、 C、 -1 D、 -18. 如图,正方体的棱长为4,动点 , 在棱上,且 , 动点在棱上,则三棱锥的体积( )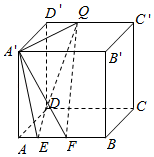 A、与点 , 位置有关 B、与点位置有关 C、与点 , , 位置有关 D、与点 , , 位置均无关,是定值9. 如图F1、F2是椭圆C1: +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
A、与点 , 位置有关 B、与点位置有关 C、与点 , , 位置有关 D、与点 , , 位置均无关,是定值9. 如图F1、F2是椭圆C1: +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )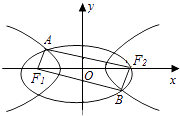 A、 B、 C、 D、10. 已知点集 , 当取遍任何实数时,所扫过的平面区域面积是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知点集 , 当取遍任何实数时,所扫过的平面区域面积是( )A、 B、 C、 D、二、填空题:本大题共5小题,每小题5分,共25分.
-
11. 直线 的倾斜角为 .12. 若直线 与直线 平行,则 .13. 若直线过点且与双曲线仅有一个公共点,则这样的直线有条14. 已知AB为圆O: 的直径,点P为椭圆 上一动点,则 的最小值为 .15. 2021年3月30日,我国某公司启用了具备“超椭圆”数学之美的全新.据了解,新将原本方正的橙色边框换成了圆角边框.这种由方到圆的弧度变化,为公司的文化融入了东方哲学的思想,赋予了品牌生命的律动感,而设计师的灵感来源于数学中的曲线 , 请将说法正确的序号填在横线上.
①对任意的 , 曲线总关于原点成中心对称;
②当时,曲线总过四个整点(横、纵坐标都为整数的点);
③当时,曲线围成图形的面积最大值为2;
④当时,曲线上的点到原点距离的最小值为2.
三、解答题:本大题共4小题,共45分.解答应写出文字说明,演算步骤或证明过程.
-
16. 已知椭圆: , 直线交椭圆于两点.(1)、求椭圆的焦点坐标及长轴长;(2)、求以线段为直径的圆的方程.17. 已知点 , 动点P 满足:|PA|=2|PB|.(1)、若点P的轨迹为曲线 , 求此曲线的方程;(2)、若点Q在直线l1: x+y+3=0上,直线l2经过点Q且与曲线只有一个公共点M,求|QM|的最小值.