山东省春季高考济南市2024年高三第一次模拟试卷
试卷更新日期:2024-01-20 类型:高考模拟
一、选择题(本大题20个小题,每小题3分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出.并填涂在答题卡上)
-
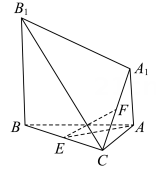
1. 已知集合 , 则等于( )A、 B、 C、 D、2. 已知命题 , 则为( )A、 B、 C、 D、3. 若 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数 的定义域为( )A、 B、 C、 D、5. 下列立体图形中,主视图和左视图不一样的是( )A、
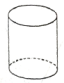 B、
B、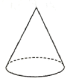 C、
C、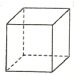 D、
D、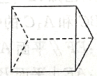 6. 下列函数中,在区间 上为增函数的是( )A、 B、 C、 D、7. 已知函数是定义在上的奇函数,当时, , 则等于( )A、 B、 C、0 D、28. 设 , 则等于( )A、 B、 C、 D、9. 已知数列是首项为1,公差为3的等差数列,如果 , 则等于( )A、677 B、676 C、675 D、67410. 4名男生和3名女生排成一排照相,要求男生和男生互不相邻,女生与女生也互不相邻,则不同的排法种数是( )A、36 B、72 C、81 D、14411. 下列式子的化简结果错误的是( )A、 B、 C、 D、12. 已知向量 , 且 , 则实数的值为( )A、1 B、 C、2 D、13. 如图所示,在平面直角坐标系中,角的终边与单位圆交于点 , 且点的纵坐标为 , 则的值为( )
6. 下列函数中,在区间 上为增函数的是( )A、 B、 C、 D、7. 已知函数是定义在上的奇函数,当时, , 则等于( )A、 B、 C、0 D、28. 设 , 则等于( )A、 B、 C、 D、9. 已知数列是首项为1,公差为3的等差数列,如果 , 则等于( )A、677 B、676 C、675 D、67410. 4名男生和3名女生排成一排照相,要求男生和男生互不相邻,女生与女生也互不相邻,则不同的排法种数是( )A、36 B、72 C、81 D、14411. 下列式子的化简结果错误的是( )A、 B、 C、 D、12. 已知向量 , 且 , 则实数的值为( )A、1 B、 C、2 D、13. 如图所示,在平面直角坐标系中,角的终边与单位圆交于点 , 且点的纵坐标为 , 则的值为( )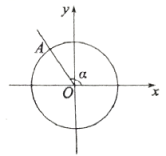 A、 B、 C、 D、14. 已知角 , 且 , 则的值为( )A、 B、 C、 D、15. 下列命题:
A、 B、 C、 D、14. 已知角 , 且 , 则的值为( )A、 B、 C、 D、15. 下列命题:①如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直;
②如果平面和不在这个平面内的直线都垂直于平面 , 那么;
③垂直同一平面的两个平面互相平行;
④垂直同一平面的两个平面互相垂直.
其中正确命题的个数是( )
A、1 B、2 C、3 D、416. 有4张卡片(除颜色外无差别),颜色分别为红、黄、蓝、绿,从这4张卡片中任取2张不同颜色的卡片,则取出的2张卡片中含有红色卡片的概率为( )A、 B、 C、 D、17. 二项式的展开式中,含项的系数是( )A、 B、462 C、792 D、18. 若圆的圆心在抛物线上,则该抛物线的焦点坐标为( )A、 B、 C、 D、19. 已知的内角的对边分别是 , 面积为S , 且 , 则角的值为( )A、 B、 C、 D、20. 陀螺起源于我国,在山西夏县新石器时代的遗址中,就出土了目前发现的最早的石制陀螺因此,陀螺的历史至少也有四千年,如图所示为一个陀螺的立体结构图,若该陀螺底面圆的直径 , 圆柱体部分的高 , 圆锥体部分的高 , 则这个陀螺的表面积是( )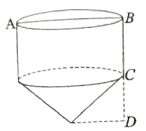 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题5个小题,每小题4分,共20分.请将答案填在答题卡相应题号的横线上)
-
21. 不等式的解集是 .22. 已知直线与圆交于A,B两点,则线段的垂直平分线的方程为 .23. 变量x,y满足的约束条件表示的可行域(阴影部分)如图所示,则目标函数的最大值是 .
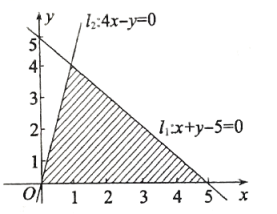 24. 为了解某中职学校男生的身体发育情况,对随机抽取的100名男生的身高进行了测量(结果精确到),并绘制了如图所示的频率分布直方图,由图可知,其中身高超过的男生的人数为 .
24. 为了解某中职学校男生的身体发育情况,对随机抽取的100名男生的身高进行了测量(结果精确到),并绘制了如图所示的频率分布直方图,由图可知,其中身高超过的男生的人数为 .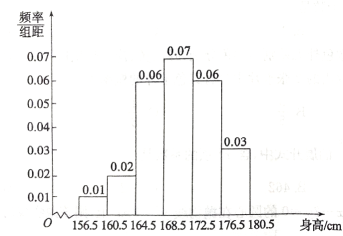 25. 已知双曲线的一条渐近线与直线垂直,则双曲线的离心率为 .
25. 已知双曲线的一条渐近线与直线垂直,则双曲线的离心率为 .三、解答题(本大题5个小题,共40分)
-
26. 已知二次函数满足 , 顶点为 .(1)、求函数的解析式;(2)、若函数在区间上单调递增,求实数的取值范围.27. 假设某市2023年新建住房400万平方米,其中有250万平方米是中、低价房.预计在今后的若干年内,该市每年新建住房面积平均比上年增长8%.另外,每年新建住房中,中、低价房的面积均比上一年增加50万平方米.求:(1)、截至到2032年底,该市所建中、低价房的面积累计(以2023年为累计的第一年)为多少万平方米?(2)、哪一年底,当年建造的中、低价房的面积占该年建造住房面积的比例首次大于85%?