重庆市巴南区2024届高三上学期数学诊断考试(一)试卷
试卷更新日期:2024-01-20 类型:高考模拟
一、选择题(共8小题,每小题5分,共40分)
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知复数 , 则( )A、 B、 C、 D、3. 已知 , 则( )A、 B、 C、 D、4. 数学来源于生活,约3000年以前,我国人民就创造出了属于自己的计数方法.十进制的算筹计数法就是中国数学史上一个伟大的创造,算筹实际上是一根根同长短的小木棍.下图是利用算筹表示数1~9的一种方法.例如:3可表示为“”,26可表示为“”,现有5根算筹,据此表示方法,若算筹不能剩余,则用1~9这9个数字表示的所有两位数中,个位数与十位数之和为5的概率是( )
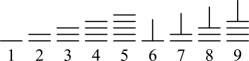 A、 B、 C、 D、5. 若数列的前项积 , 则的最大值与最小值的和为( )A、 B、 C、2 D、36. 如图所示,正方形的边长为2,点 , , 分别是边 , , 的中点,点是线段上的动点,则的最小值为( )
A、 B、 C、 D、5. 若数列的前项积 , 则的最大值与最小值的和为( )A、 B、 C、2 D、36. 如图所示,正方形的边长为2,点 , , 分别是边 , , 的中点,点是线段上的动点,则的最小值为( )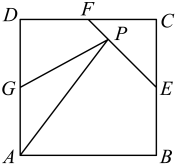 A、 B、3 C、 D、487. 椭圆的左右焦点为 , , 点P为椭圆上不在坐标轴上的一点,点M , N满足 , , 若四边形的周长等于 , 则椭圆C的离心率为( )A、 B、 C、 D、8. 已知偶函数满足 , , 且当时,.若关于的不等式在上有且只有个整数解,则实数的取值范围是( )A、 B、 C、 D、
A、 B、3 C、 D、487. 椭圆的左右焦点为 , , 点P为椭圆上不在坐标轴上的一点,点M , N满足 , , 若四边形的周长等于 , 则椭圆C的离心率为( )A、 B、 C、 D、8. 已知偶函数满足 , , 且当时,.若关于的不等式在上有且只有个整数解,则实数的取值范围是( )A、 B、 C、 D、二、多选题(共4小题,每小题5分,共20分)
-
9. 已知函数 , 则( )A、 B、的最小正周期为 C、在上单调递减 D、在上单调递增10. 某市为响应教育部《切实保证中小学每天一小时校园体育活动的规定》号召,提出“保证中小学生每天一小时校园体育活动”的倡议.在某次调研中,甲、乙两个学校学生一周的运动时间统计如下表:
学校
人数
平均运动时间
方差
甲校
2000
10
3
乙校
3000
8
2
记这两个学校学生一周运动的总平均时间为 , 方差为 , 则( )
A、 B、 C、 D、11. 如图,平行六面体中, , , 与交于点O , 则下列说法正确的有( )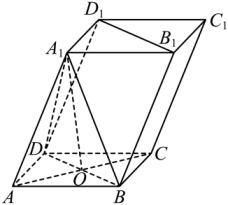 A、平面平面 B、若 , 则平行六面体的体积 C、 D、若 , 则12. 已知函数 , 下列选项正确的是( )A、有最大值 B、 C、若时,恒成立,则 D、设为两个不相等的正数,且 , 则
A、平面平面 B、若 , 则平行六面体的体积 C、 D、若 , 则12. 已知函数 , 下列选项正确的是( )A、有最大值 B、 C、若时,恒成立,则 D、设为两个不相等的正数,且 , 则三、填空题(共4小题,每小题5分,共20分)
-
13. 展开式中的各二项式系数之和为256,则的系数是14. 现从甲、乙、丙3人中选派一人参加“垃圾分类”知识竞答,他们商议通过玩“石头、剪刀、布”游戏解决:如果其中两人手势相同,另一人不同,则选派手势不同的人参加;否则重新进行一局“石头、剪刀、布”游戏,直到确定人选为止.在每局游戏中,甲、乙、丙各自出3种手势是等可能的,且各局游戏是相互独立的,则直到第三局游戏才最终确定选派人员的概率为.15. 已知等比数列满足: , .数列满足 , 其前项和为 , 若恒成立,则的最小值为.16. 已知抛物线上存在两点(异于坐标原点),使得 , 直线AB与x轴交于M点,将直线AB绕着M点逆时针旋转与该抛物线交于C , D两点,则四边形ACBD面积的最小值为.
四、解答题(共6小题,共70分)
-
17. 在中,角所对的边分别为 , .(1)、求角;(2)、若的面积为 , 且 , 求的周长.18. 已知数列的首项 , 且满足.(1)、求证:是等比数列;(2)、求数列的前项和.19. 书籍是精神世界的入口,阅读让精神世界闪光,阅读逐渐成为许多人的一种生活习惯,每年4月23日为世界读书日.某研究机构为了解某地年轻人的阅读情况,通过随机抽样调查了位年轻人,对这些人每天的阅读时间(单位:分钟)进行统计,得到样本的频率分布直方图,如图所示.
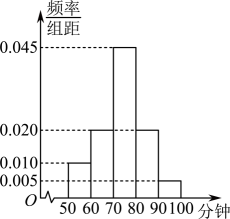 (1)、根据频率分布直方图,估计这位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)(2)、若年轻人每天阅读时间近似地服从正态分布 , 其中近似为样本平均数 , 求;(3)、为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组 , , 的年轻人中抽取10人,再从中任选3人进行调查,求抽到每天阅读时间位于的人数的分布列和数学期望.
(1)、根据频率分布直方图,估计这位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)(2)、若年轻人每天阅读时间近似地服从正态分布 , 其中近似为样本平均数 , 求;(3)、为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组 , , 的年轻人中抽取10人,再从中任选3人进行调查,求抽到每天阅读时间位于的人数的分布列和数学期望.附参考数据:若,则①;②;③.
20. 如图所示,在三棱锥中,已知平面 , 平面平面 . (1)、证明:平面;(2)、若 , , 在线段上(不含端点),是否存在点 , 使得二面角的余弦值为 , 若存在,确定点的位置;若不存在,说明理由.
(1)、证明:平面;(2)、若 , , 在线段上(不含端点),是否存在点 , 使得二面角的余弦值为 , 若存在,确定点的位置;若不存在,说明理由.