黑龙江省鸡西市密山市高级名校2023-2024学年高二上学期数学期末联考试卷
试卷更新日期:2024-01-20 类型:期末考试
一、选择题(每题5分,共40分)
-
1. 已知椭圆C: , 则椭圆C的长轴长为( )A、3 B、4 C、6 D、92. 如果存在三个不全为零的实数x、y、z , 使得 , 则关于、、( )A、两两相互垂直 B、只有两个向量互相垂直 C、共面 D、有两个向量互相平行3. 抛物线 的准线方程为( )A、 B、 C、 D、4. 如图,某建筑物白色的波浪形屋顶像翅膀一样漂浮,建筑师通过双曲线的设计元素赋予了这座建筑以轻盈,极简和雕塑般的气质,该建筑物外形弧线的一段可以近似看成焦点在y轴上的双曲线上支的一部分.已知该双曲线的上焦点F到下顶点的距离为18,F到渐近线的距离为6,则该双曲线的离心率为( ).
 A、 B、 C、 D、5. 由伦敦著名建筑事务所SteynStudio设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )
A、 B、 C、 D、5. 由伦敦著名建筑事务所SteynStudio设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( ) A、 B、 C、 D、6. 2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组 , 第二组 , …,第六组 , 得到如下频率分布直方图,则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )
A、 B、 C、 D、6. 2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组 , 第二组 , …,第六组 , 得到如下频率分布直方图,则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )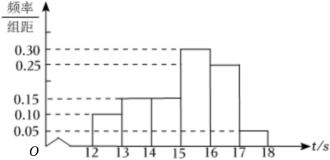 A、15.2 15.4 B、15.1 15.4 C、15.1 15.3 D、15.2 15.37. 某企业为了研究某种产品的销售价格(元)与销售量(千件)之间的关系,通过大量市场调研收集得到以下数据:
A、15.2 15.4 B、15.1 15.4 C、15.1 15.3 D、15.2 15.37. 某企业为了研究某种产品的销售价格(元)与销售量(千件)之间的关系,通过大量市场调研收集得到以下数据:16
12
8
4
24
a
38
64
其中某一项数据※丢失,只记得这组数据拟合出的线性回归方程为: , 则缺失的数据a是( )
A、33 B、35 C、34 D、34.88. 十七世纪法国数学家皮埃尔•德•费马提出的一个著名的几何问题:“已知一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小”.它的答案是:当三角形的三个角均小于时,即该点与三角形的三个顶点的连线两两成角;当三角形有一内角大于或等于时,所求点为三角形最大内角的顶点,在费马问题中,所求点称为费马点.已知在中, , 是的角平分线,交于 , 满足若为的费马点,则( )A、 B、 C、 D、二、多项选择题(答对一项得1.5分,满分18分)
-
9. 给出下列命题,其中正确命题有( )A、空间任意三个不共面的向量都可以作为一个基底 B、已知向量 , 则存在向量可以与 , 构成空间的一个基底 C、 , , , 是空间四点若不能构成空间的一个基底那么 , , , 共面 D、已知向量组是空间的一个基底,若 , 则也是空间的一个基底10. 已知正四棱柱的底面边为1,侧棱长为 , 是的中点,则( )
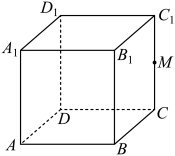 A、任意 , B、存在 , 直线与直线相交 C、平面与底面交线长为定值 D、当时,三棱锥外接球表面积为11. 若动点、分别在直线与上移动,则的中点到原点的距离可能为( )A、 B、 C、 D、12. 已知抛物线:()的焦点到准线的距离为2,过的直线交抛物线于两点 , , 则( )A、的准线方程为 B、若 , 则 C、若 , 则的斜率为 D、过点作准线的垂线,垂足为 , 若轴平分 , 则
A、任意 , B、存在 , 直线与直线相交 C、平面与底面交线长为定值 D、当时,三棱锥外接球表面积为11. 若动点、分别在直线与上移动,则的中点到原点的距离可能为( )A、 B、 C、 D、12. 已知抛物线:()的焦点到准线的距离为2,过的直线交抛物线于两点 , , 则( )A、的准线方程为 B、若 , 则 C、若 , 则的斜率为 D、过点作准线的垂线,垂足为 , 若轴平分 , 则三、解答题
-
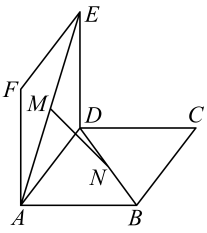
13. 已知的展开式中,前三项系数的绝对值依次成等差数列,(1)、求展开式中二项式系数最大的项;(2)、求展开式中所有的有理项.14. 如图,在多面体中,四边形是正方形, , , 为的中点.
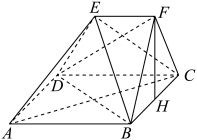 (1)、求证:平面;(2)、求证:平面;(3)、求二面角的大小.15. 已知直线.(1)、若不经过第三象限,求的取值范围;(2)、求坐标原点到直线距离的最小值,并求此时直线的方程.16. 如图,在多面体中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E , F两点,上、下底面矩形的长、宽分别为c , d与a , b , 且a>c , b>d , 两底面间的距离为h .
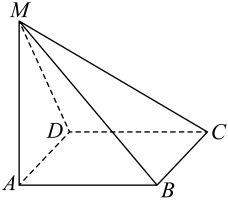
(1)、求证:平面;(2)、求证:平面;(3)、求二面角的大小.15. 已知直线.(1)、若不经过第三象限,求的取值范围;(2)、求坐标原点到直线距离的最小值,并求此时直线的方程.16. 如图,在多面体中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E , F两点,上、下底面矩形的长、宽分别为c , d与a , b , 且a>c , b>d , 两底面间的距离为h .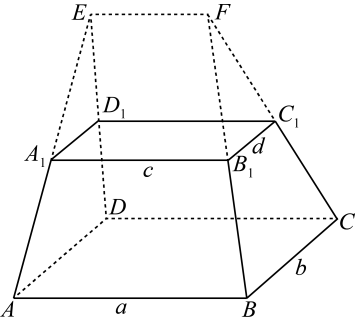 (1)、求侧面与底面所成二面角的大小;(2)、证明:;(3)、在估测该多面体的体积时,经常运用近似公式来计算,已知它的体积公式是 , 试判断与V的大小关系,并加以证明.
(1)、求侧面与底面所成二面角的大小;(2)、证明:;(3)、在估测该多面体的体积时,经常运用近似公式来计算,已知它的体积公式是 , 试判断与V的大小关系,并加以证明.注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.