湖北省荆州市公安县2023-2024学年高三上学期1月质检模拟1数学试题
试卷更新日期:2024-01-20 类型:高考模拟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 , 集合 , 则A、 B、 C、 D、2. 已知复数满足(其中是虚数单位),则的虚部是( )A、-1 B、1 C、 D、3. 已知直线的一个方向向量为 , 且经过点 , 则的方程为( )A、 B、 C、 D、4. 若不等式对任意恒成立,则实数的取值范围为( )A、 B、 C、 D、5. 已知椭圆和双曲线的公共焦点为 , 在第一象限内的交点为 , 则( )A、-4 B、-6 C、-8 D、-96. 将甲,乙,丙,丁,戊五名志愿者安排到四个社区进行暑期社会实践活动,要求每个社区至少安排一名志愿者,那甲恰好被安排在社区的不同安排方法数为( )A、24 B、36 C、60 D、967. 已知公比不为1的等比数列的前项和为 , 记:为等差数列;:对任意自然数为等差数列,则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件8. 在平面直角坐标系中,设都是锐角,若的始边都与轴的非负半轴重合,终边分别与圆交于点 , 且满足 , 则当最大时,的值为( )A、 B、 C、 D、
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 某中学选派甲、乙、丙、丁、戊5位同学参加数学竞赛,他们的成绩统计如下:
学生
甲
乙
丙
丁
戊
成绩
则下列结论正确的为
A、这位同学成绩的中位数是 B、这位同学成绩的平均数是 C、这位同学成绩的第百分位数是 D、若去掉戊的成绩,则剩余四人成绩的方差保持不变10. 已知直线和圆 , 则( )A、直线过定点 B、直线与圆有两个交点 C、存在直线与直线垂直 D、直线被圆截得的最短弦长为11. 若函数既有极大值也有极小值,则( )A、 B、 C、 D、12. 下列物体,能够被半径为的球体完全容纳的有( )A、所有棱长均为的四面体 B、底面棱长为 , 高为的正六棱锥 C、底面直径为 , 高为的圆柱 D、上、下底面的边长分别为 , 高为的正四棱台三、填空题:本题共4小题,每小题5分,共20分.
-
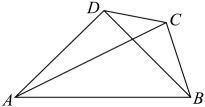
13. 的展开式中含的项的系数为.14. 已知向量 , 的夹角为 , 且 , 则向量在向量上的投影向量为.用表示15. 定义在上的可导函数满足:①;②值域为;③对任意 , 有及 , 请写出同时满足上述所有条件的一个函数解析式:.16. 如图,在平面凸四边形中, , , , , 为钝角,则对角线的最大值为.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
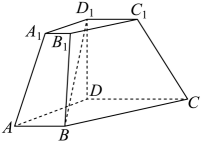
17. 已知的内角的对边分别为 , 且的面积为(1)、求;(2)、求周长的最小值.18. 已知数列满足 , , 且数列是等差数列.(1)、求数列的通项公式;(2)、求数列的前项和.19. 如图,在四棱台中,已知 , .
 (1)、证明:平面;(2)、若四棱台的体积为 , 求二面角的余弦值.20. 设双曲线的离心率为 , 且顶点到渐近线的距离为.已知直线过点 , 直线与双曲线的左,右两支的交点分别为 , 直线与双曲线的渐近线的交点为 , 其中点在轴的右侧.设的面积分别是.(1)、求双曲线的方程;(2)、求的取值范围.21. 某公司为激励员工,在年会活动中,该公司的位员工通过摸球游戏抽奖,其游戏规则为:每位员工前面都有1个暗盒,第1个暗盒里有3个红球与1个白球.其余暗盒里都恰有2个红球与1个白球,这些球的形状大小都完全相同.第1位员工从第1个暗盒里取出1个球,并将这个球放入第2个暗盒里,第2位员工再从第2个暗盒里面取出1个球并放入第3个暗盒里,依次类推,第n-1位员工再从第n-1个暗盒里面取出1个球并放入第个暗盒里.第位员工从第个暗盒中取出1个球,游戏结束.若某员工取出的球为红球,则该员工获得奖金1000元,否则该员工获得奖金500元.设第位员工获得奖金为元.(1)、求的概率;(2)、求的数学期望 , 并指出第几位员工获得奖金额的数学期望最大.22. 已知函数.(1)、若 , 求证:当时,;(2)、讨论函数在区间上的零点个数.
(1)、证明:平面;(2)、若四棱台的体积为 , 求二面角的余弦值.20. 设双曲线的离心率为 , 且顶点到渐近线的距离为.已知直线过点 , 直线与双曲线的左,右两支的交点分别为 , 直线与双曲线的渐近线的交点为 , 其中点在轴的右侧.设的面积分别是.(1)、求双曲线的方程;(2)、求的取值范围.21. 某公司为激励员工,在年会活动中,该公司的位员工通过摸球游戏抽奖,其游戏规则为:每位员工前面都有1个暗盒,第1个暗盒里有3个红球与1个白球.其余暗盒里都恰有2个红球与1个白球,这些球的形状大小都完全相同.第1位员工从第1个暗盒里取出1个球,并将这个球放入第2个暗盒里,第2位员工再从第2个暗盒里面取出1个球并放入第3个暗盒里,依次类推,第n-1位员工再从第n-1个暗盒里面取出1个球并放入第个暗盒里.第位员工从第个暗盒中取出1个球,游戏结束.若某员工取出的球为红球,则该员工获得奖金1000元,否则该员工获得奖金500元.设第位员工获得奖金为元.(1)、求的概率;(2)、求的数学期望 , 并指出第几位员工获得奖金额的数学期望最大.22. 已知函数.(1)、若 , 求证:当时,;(2)、讨论函数在区间上的零点个数.