山东省潍坊市昌乐县2023-2024学年高三上学期1月模拟预测数学试题

试卷更新日期：2024-01-20 类型：高考模拟

进入出卷网下载

一、单项选择题：本题共8小题。每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知复数z满足 $\frac{1 + i}{z} = 1 - i$ ，则 $| z | =$ （）

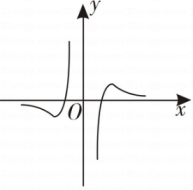
A、 $2 \sqrt{2}$ B、2 C、 $\sqrt{2}$ D、1

查看试题解析
2. 若全集U=R，集合 $A = {x \in Z | x_{}^{2} < 16}$ ， $B = {x | x - 1 \leq 0}$ ，则 $A \cap (C_{U}^{} B) =$ （）

A、{1，2，3} B、{2，3} C、 ${x | 1 \leq x < 4}$ D、 ${x | 1 < x < 4}$

查看试题解析
3. 已知向量 $\vec{O A} = (3 ， - 4) ， \vec{O B} = (6 ， - 3) ， \vec{O C} = (2 m ， m + 1) ，若 \vec{A B} / / \vec{O C}$ ，则实数m的值为（）

A、 $\frac{1}{5}$ B、 $- \frac{3}{5}$ C、 $- 3$ D、 $- \frac{1}{7}$

查看试题解析
4. 函数 $f (x) = \frac{l n | x |}{x^{3}}$ 的部分图象大致为（）

A、 B、 C、 D、

查看试题解析
5. “ $a < - 1$ ”是“ $\exists x_{0} \in R ， a s i n x_{0} + 1 < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 若 $l o g_{3} (2 a + b) = 1 + l o g_{\sqrt{3}} \sqrt{a b}$ ，则 $a + 2 b$ 的最小值为（）

A、6 B、 $\frac{8}{3}$ C、3 D、 $\frac{16}{3}$

查看试题解析
7. 已知圆 $C ： x_{}^{2} + y_{}^{2} - 10 x + 21 = 0$ 与双曲线 $\frac{y_{}^{2}}{a_{}^{2}} - \frac{x_{}^{2}}{b_{}^{2}} = 1 (a > 0 ， b > 0)$ 的渐近线相切，则该双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\frac{5}{3}$ C、 $\frac{5}{2}$ D、 $\sqrt{5}$

查看试题解析
8. 定义在 $R$ 上函数 $f (x)$ 满足 $f (- x) = f (x)$ ，且对任意的不相等的实数 $x_{1} ， x_{2} \in [0 ， + \infty)$ 有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ 成立，若关于x的不等式 $f (2 m x - ln x - 3) \geq 2 f (3) - f (- 2 m x + ln x + 3)$ 在 $x \in [1 ， 3]$ 上恒成立，则实数m的取值范围是（）

A、 $[\frac{1}{2 e} ， 1 + \frac{ln 6}{6}]$ B、 $[\frac{1}{2 e} ， 1 + \frac{ln 3}{6}]$ C、 $[\frac{1}{e} ， 2 + \frac{ln 3}{3}]$ D、 $[\frac{1}{e} ， 2 + \frac{ln 6}{3}]$

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得3分，有选错的得0分．

9. 已知 $a ， b ， c ， d$ 均为实数，则下列命题正确的是（）

A、若 $a > b ， c > d$ ，则 $a c > b d$ B、若 $a b > 0 ， b c - a d > 0$ ，则 $\frac{c}{a} - \frac{d}{b} > 0$ C、若 $a > b ， c > d ，$ 则 $a - d > b - c$ D、若 $a > b ， c > d > 0 ，$ 则 $\frac{a}{d} > \frac{b}{c}$

查看试题解析
10. 已知函数 $f (x) = \sin (3 x + φ) (- \frac{π}{2} < φ < \frac{π}{2})$ 的图象关于直线 $x = \frac{π}{4}$ 对称，则（）

A、函数 $f (x + \frac{π}{12})$ 为奇函数 B、函数 $f (x)$ 在 $[\frac{π}{12} ， \frac{π}{3}]$ 上单调递增 C、若 $| f (x_{1}) - f (x_{2}) | = 2$ ，则 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{3}$ D、函数 $f (x)$ 的图象向右平移 $\frac{π}{4}$ 个单位长度得到函数 $y = - \cos 3 x$ 的图象

查看试题解析
11. 甲、乙两类水果的质量（单位： $k g$ ）分别服从正态分布 $N (μ_{1}^{} ， {δ_{1}^{}}_{}^{2})$ ， $N (μ_{2}^{} ， {δ_{2}^{}}_{}^{2})$ ，其正态分布的密度曲线如图所示，则下列说法正确的是（）

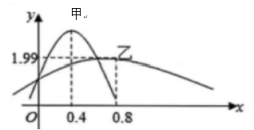A、甲类水果的平均质量 $μ_{1}^{} = 0.4 k g$ B、甲类水果的质量比乙类水果的质量更集中于平均值左右 C、甲类水果的平均质量比乙类水果的平均质量小 D、乙类水果的质量服从的正态分布的参数 $δ_{2}^{} = 1.99$

查看试题解析
12. 如图，在边长为2的正方形AP₁P₂P₃中，线段BC的端点B，C分别在边P₁P₂ ， P₂P₃上滑动，且P₂B＝P₂C＝x。现将△AP₁B，△AP₃C分别沿AB，CA折起使点P₁ ， P₃重合，重合后记为点P，得到三棱锥P－ABC。现有以下结论：（）

A、AP⊥平面PBC B、当B，C分别为P₁P₂ ， P₂P₃的中点时，三棱锥P－ABC的外接球的表面积为6π C、x的取值范围为(0，4－2 $\sqrt{2}$ ) D、三棱锥P－ABC体积的最大值为 $\frac{1}{3}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯．

查看试题解析
14. 从分别标有，2，…，9的9张卡片中不放回地随机抽取2次，每次抽取1张．则抽到的2张卡片上的数奇偶性不同的概率是．

查看试题解析
15. 已知抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点为F(4，0)，过F作直线l交抛物线于M ， N两点，则p= ， $\frac{| N F |}{9} - \frac{4}{| M F |}$ 的最小值为．

查看试题解析
16. 设函数 $f (x)$ 在定义域(0，+∞)上是单调函数， $\forall x \in (0 ， + \infty) ， f [f (x) - e^{x} + x] = e$ ，若不等式 $f (x) + f^{'} (x) \geq a x 对 x \in (0 ， + \infty)$ 恒成立，则实数a的取值范围是．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 已知函数 $f (x) = l o g_{k} x$ （ $k$ 为常数， $k > 0$ 且 $k \neq 1$ ）.

(1)、在下列条件中选择一个使数列 ${a_{n}}$ 是等比数列，说明理由；
①数列 ${f (a_{n})}$ 是首项为2，公比为2的等比数列；②数列 ${f (a_{n})}$ 是首项为 $4$ ，公差为 $2$ 的等差数列；③数列 ${f (a_{n})}$ 是首项为2，公差为2的等差数列的前n项构成的数列.

(2)、设 $a_{n} b_{n} = \frac{2^{n + 1}}{4 n^{2} - 1}$ ，当 $k = \sqrt{2}$ 时，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ， .

查看试题解析
18. 在△ABC中，内角A，B，C所对的边分别为 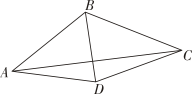$a ， b ， c$ ，已知 $b + c = 2 a$ ， $5 c s i n B = 7 a s i n C$ .

(1)、求角 $B$ ；

(2)、如图所示， $B D$ 平分 $∠ A B C$ ，且 $∠ D A B = 45 °$ ， $B C = 4$ ，求△BCD的面积。

查看试题解析
19. 如图，四棱锥P－ABCD中，PA⊥底面ABCD ，底面ABCD是直角梯形，∠ADC＝90°，AD∥BC ， AB⊥AC ， AB＝AC＝ $\sqrt{2}$ ，点E在AD上，且AE＝2ED.

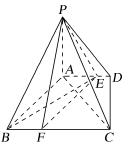(1)、已知点F在BC上，且CF＝2FB ，求证：平面PEF⊥平面PAC；

(2)、当二面角A－PB－E的余弦值为多少时，直线PC与平面PAB所成的角为45°？

查看试题解析
20. 某企业拥有3条相同的生产线，每条生产线每月至多出现一次故障．各条生产线是否出现故障相互独立，且出现故障的概率为 $\frac{1}{3}$ ．

(1)、求该企业每月有且只有1条生产线出现故障的概率；

(2)、为提高生产效益，该企业决定招聘n名维修工人及时对出现故障的生产线进行维修．已知每名维修工人每月只有及时维修1条生产线的能力，且每月固定工资为1万元．此外，统计表明，每月在不出现故障的情况下，每条生产线创造12万元的利润；如果出现故障能及时维修，每条生产线创造8万元的利润；如果出现故障不能及时维修，该生产线将不创造利润．以该企业每月实际获利的期望值为决策依据，在 $n = 1$ 与 $n = 2$ 之中选其一，应选用哪个?(实际获利=生产线创造利润－维修工人工资)

查看试题解析
21. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率e满足 $2 e^{2} - 3 \sqrt{2} e + 2 = 0$ ，右顶点为A，上顶点为B，点C(0，－2)，过点C作一条与y轴不重合的直线l ，直线l交椭圆E于P，Q两点，直线BP，BQ分别交x轴于点M，N；当直线l经过点A时，l的斜率为 $\sqrt{2}$ ．

(1)、求椭圆E的方程；

(2)、证明： $S_{Δ B O M} \cdot S_{Δ B C N}$ 为定值．

查看试题解析
22. 已知函数 $f (x) = e^{x} - a x$ ．

(1)、当 $a > 0$ 时，设函数 $f (x)$ 的最小值为 $g (a)$ ，证明： $g (a) \leq 1$ ；

(2)、若函数 $h (x) = f (x) - \frac{1}{2} x^{2}$ 。有两个极值点 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，
证明： $h (x_{1}) + h (x_{2}) > 2$ ．

查看试题解析