江西省2023-2024学年高三上学期1月新高考“七省联考”考前数学猜题卷一
试卷更新日期:2024-01-20 类型:高考模拟
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
-
1. 设 , 则“”是“”的( )A、必要而不充分条件 B、充分而不必要条件 C、充要条件 D、既不充分也不必要条件2. 下列关于复数的说法,正确的是( )A、复数是最小的纯虚数 B、在复数范围内,模为1的复数共有和四个 C、与是一对共轭复数 D、虚轴上的点都表示纯虚数3. 已知圆的半径为2,弦的长为 , 若 , 则( )A、-4 B、-2 C、2 D、44. 调和信号是指频率恒定的一种信号,三角函数性质可以表达调和信号的周期性,指数函数可用来描述信号的衰减.已知一个调和信号的函数为 , 它的图象大致为( )A、
 B、
B、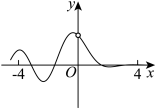 C、
C、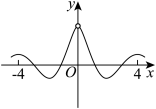 D、
D、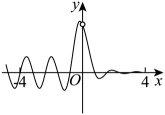 5. 折纸与剪纸是一种用纸张折成或剪成各种不同形状的艺术活动,是我们中华民族的传统文化,历史悠久,内涵博大精深,世代传承.现将一张腰长为1的等腰直角三角形纸,每次对折后仍成等腰直角三角形,对折5次,然后用剪刀剪下其内切圆,则可得到若干个相同的圆片纸,这些圆片纸的半径为( )A、 B、 C、 D、6. 已知双曲线 , 直线与双曲线交于A , B两点,为坐标原点,若点在直线上且直线OP把分成面积相等的两部分,则下列不能作为点的坐标的是( )A、 B、 C、 D、7. 已知半径为的球中有一个内接正四棱锥,底面边长为 , 当正四棱锥的高为时,正四棱锥的体积取得最大值 , 则( )A、 B、 C、 D、8. 设正数满足 , 当时,恒有 , 则乘积的最小值是( )A、 B、2 C、 D、
5. 折纸与剪纸是一种用纸张折成或剪成各种不同形状的艺术活动,是我们中华民族的传统文化,历史悠久,内涵博大精深,世代传承.现将一张腰长为1的等腰直角三角形纸,每次对折后仍成等腰直角三角形,对折5次,然后用剪刀剪下其内切圆,则可得到若干个相同的圆片纸,这些圆片纸的半径为( )A、 B、 C、 D、6. 已知双曲线 , 直线与双曲线交于A , B两点,为坐标原点,若点在直线上且直线OP把分成面积相等的两部分,则下列不能作为点的坐标的是( )A、 B、 C、 D、7. 已知半径为的球中有一个内接正四棱锥,底面边长为 , 当正四棱锥的高为时,正四棱锥的体积取得最大值 , 则( )A、 B、 C、 D、8. 设正数满足 , 当时,恒有 , 则乘积的最小值是( )A、 B、2 C、 D、二、多选题(共20分)
-
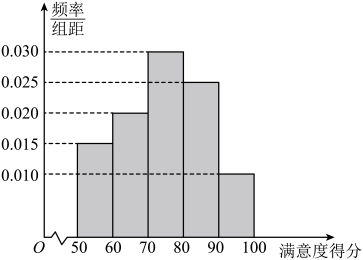
9. 近年来,网络消费新业态、新应用不断涌现,消费场景也随之加速拓展,某报社开展了网络交易消费者满意度调查,某县人口约为万人,从该县随机选取人进行问卷调查,根据满意度得分分成以下组:、、、 , 统计结果如图所示.由频率分布直方图可认为满意度得分(单位:分)近似地服从正态分布 , 且 , , , 其中近似为样本平均数,近似为样本的标准差 , 并已求得.则( )
 A、由直方图可估计样本的平均数约为 B、由直方图可估计样本的中位数约为 C、由正态分布可估计全县的人数约为万人 D、由正态分布可估计全县的人数约为万人10. 已知圆 , 直线(且不同时为0),下列说法正确的是( )A、当直线经过时,直线与圆相交所得弦长为 B、当时,直线与关于点对称,则的方程为: C、当时,圆上存在4个点到直线的距离为 D、过点与平行的直线方程为:11. 在棱长为2的正方体中, , 点M为棱上一动点(可与端点重合),则( )A、当点M与点A重合时,四点共面且 B、当点M与点B重合时, C、当点M为棱的中点时,平面 D、直线与平面所成角的正弦值存在最小值12. 已知实数m , n满足 , 且 , 则( )A、 B、 C、 D、
A、由直方图可估计样本的平均数约为 B、由直方图可估计样本的中位数约为 C、由正态分布可估计全县的人数约为万人 D、由正态分布可估计全县的人数约为万人10. 已知圆 , 直线(且不同时为0),下列说法正确的是( )A、当直线经过时,直线与圆相交所得弦长为 B、当时,直线与关于点对称,则的方程为: C、当时,圆上存在4个点到直线的距离为 D、过点与平行的直线方程为:11. 在棱长为2的正方体中, , 点M为棱上一动点(可与端点重合),则( )A、当点M与点A重合时,四点共面且 B、当点M与点B重合时, C、当点M为棱的中点时,平面 D、直线与平面所成角的正弦值存在最小值12. 已知实数m , n满足 , 且 , 则( )A、 B、 C、 D、三、填空题(共20分)
-
13. 在高中数学第一册我们学习“集合的子集”时知道,若一个集合有个元素,则该集合的子集(包括含有0个元素(空集),1个元素,2个元素,…,个元素)个数共有个,请你结合你所学习的二项式定理的有关知识写出关于子集个数为个的计算等式 .14. 若数列a , 27, , b , 为等比数列,则 .15. 椭圆的弦满足 , 记坐标原点在的射影为 , 则到直线的距离为1的点的个数为.16. 对 , 都有关于的不等式恒成立,则的值可以是 .
四、解答题(共70分)
-
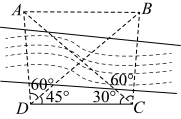
17. 如图,A、B两点都在河的对岸(不可到达),若在河岸选取相距20米的C、D两点,测得∠BCA=60°,∠ACD=30°,∠CDB=45°,∠BDA=60°,那么此时A , B两点间的距离是多少?
 18. 已知点 , , 设 , 当时,线段的中点为 , 关于直线的对称点为.例如,为线段的中点,则 , .(1)、设 , 证明:是等比数列.(2)、求数列的通项公式.19. 如图,在圆台中,截面分别交圆台的上下底面于点 , , , 四点.点为劣弧的中点.
18. 已知点 , , 设 , 当时,线段的中点为 , 关于直线的对称点为.例如,为线段的中点,则 , .(1)、设 , 证明:是等比数列.(2)、求数列的通项公式.19. 如图,在圆台中,截面分别交圆台的上下底面于点 , , , 四点.点为劣弧的中点. (1)、求过点作平面垂直于截面 , 请说明作法,并说明理由;(2)、若圆台上底面的半径为1,下底面的半径为3,母线长为3, , 求平面与平面所成夹角的余弦值.20. 多巴胺是一种神经传导物质,能够传递兴奋及开心的信息.近期很火的多巴胺穿搭是指通过服装搭配来营造愉悦感的着装风格,通过色彩艳丽的时装调动正面的情绪,是一种“积极化的联想”.小李同学紧跟潮流,她选择搭配的颜色规则如下:从红色和蓝色两种颜色中选择,用“抽小球”的方式决定衣物颜色,现有一个箱子,里面装有质地、大小一样的4个红球和2个白球,从中任取4个小球,若取出的红球比白球多,则当天穿红色,否则穿蓝色.每种颜色的衣物包括连衣裙和套装,若小李同学选择了红色,再选连衣裙的可能性为0.6,而选择了蓝色后,再选连衣裙的可能性为0.5.(1)、写出小李同学抽到红球个数的分布列及期望;(2)、求小李同学当天穿连衣裙的概率.
(1)、求过点作平面垂直于截面 , 请说明作法,并说明理由;(2)、若圆台上底面的半径为1,下底面的半径为3,母线长为3, , 求平面与平面所成夹角的余弦值.20. 多巴胺是一种神经传导物质,能够传递兴奋及开心的信息.近期很火的多巴胺穿搭是指通过服装搭配来营造愉悦感的着装风格,通过色彩艳丽的时装调动正面的情绪,是一种“积极化的联想”.小李同学紧跟潮流,她选择搭配的颜色规则如下:从红色和蓝色两种颜色中选择,用“抽小球”的方式决定衣物颜色,现有一个箱子,里面装有质地、大小一样的4个红球和2个白球,从中任取4个小球,若取出的红球比白球多,则当天穿红色,否则穿蓝色.每种颜色的衣物包括连衣裙和套装,若小李同学选择了红色,再选连衣裙的可能性为0.6,而选择了蓝色后,再选连衣裙的可能性为0.5.(1)、写出小李同学抽到红球个数的分布列及期望;(2)、求小李同学当天穿连衣裙的概率.