安徽省2024届高三上学期“七省联考” 数学模拟练习(2)
试卷更新日期:2024-01-20 类型:高考模拟
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , 集合 , 集合 , 则( )A、 B、 C、 D、2. 已知函数f(x)是定义在R上的奇函数,当 时,f(x)= , f()= ,则实数 m=( )A、 B、 C、 D、3. “基础学科拔尖学生培养试验计划”简称“珠峰计划”,是国家为回应“钱学森之间”而推出的一项人才培养计划,旨在培养中国自己的学术大师已知浙江大学、复旦大学、武汉大学、中山大学均有开设数学学科拔尖学生培养基地,某班级有位同学从中任选一所学校作为奋斗目标,则每所学校至少有一位同学选择的不同方法数共有( )A、种 B、种 C、种 D、种4. 记为等比数列的前项和,若 , , 则( )A、 B、 C、 D、5. 如图,在长方形中, , , 从上的一点发出的一束光沿着与夹角为的方向射到上的点后,依次反射到、上的、点,最后回到点,则等于( )
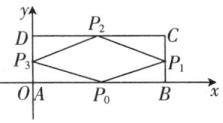 A、 B、 C、 D、6. 函数在处有极值为 , 则的值为( )A、 B、 C、 D、或7. 已知函数 , 若存在实数当时,满足则的取值范围为( )A、 B、 C、 D、8. 如图,椭圆的左焦点为 , 右顶点为 , 点在轴上,点在椭圆上,且满足轴,四边形是等腰梯形,直线与轴交于点 , 则椭圆的离心率为( )
A、 B、 C、 D、6. 函数在处有极值为 , 则的值为( )A、 B、 C、 D、或7. 已知函数 , 若存在实数当时,满足则的取值范围为( )A、 B、 C、 D、8. 如图,椭圆的左焦点为 , 右顶点为 , 点在轴上,点在椭圆上,且满足轴,四边形是等腰梯形,直线与轴交于点 , 则椭圆的离心率为( )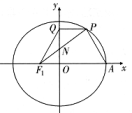 A、 B、 C、 D、
A、 B、 C、 D、二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 若复数 , , 其中是虚数单位,则下列说法正确的是( )A、 B、 C、若是纯虚数,那么 D、若 , 在复平面内对应的向量分别为 , 为坐标原点 , 则10. 如图,为圆锥底面圆的直径,点是圆上异于 , 的动点, , 则下列结论正确的是( )
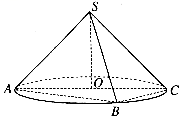 A、圆锥 的侧面积为 B、三棱锥体积的最大值为 C、的取值范围是 D、若 , 为线段上的动点,则的最小值为11. 某商场设有电子盲盒机,每个盲盒外观完全相同,规定每个玩家只能用一个账号登陆,且每次只能随机选择一个开启.已知玩家第一次抽盲盒,抽中奖品的概率为 , 从第二次抽盲盒开始,若前一次没抽中奖品,则这次抽中的概率为 , 若前一次抽中奖品,则这次抽中的概率为 . 记玩家第次抽盲盒,抽中奖品的概率为 , 则( )A、 B、数列为等比数列 C、 D、当时,越大,越小12. 已知点为抛物线的焦点,直线过点交抛物线于两点, 设为坐标原点, , 直线与轴分别交于两点,则以下选项正确的是( )A、 B、若 , 则 C、若 , 则面积的最小值为 D、四点共圆
A、圆锥 的侧面积为 B、三棱锥体积的最大值为 C、的取值范围是 D、若 , 为线段上的动点,则的最小值为11. 某商场设有电子盲盒机,每个盲盒外观完全相同,规定每个玩家只能用一个账号登陆,且每次只能随机选择一个开启.已知玩家第一次抽盲盒,抽中奖品的概率为 , 从第二次抽盲盒开始,若前一次没抽中奖品,则这次抽中的概率为 , 若前一次抽中奖品,则这次抽中的概率为 . 记玩家第次抽盲盒,抽中奖品的概率为 , 则( )A、 B、数列为等比数列 C、 D、当时,越大,越小12. 已知点为抛物线的焦点,直线过点交抛物线于两点, 设为坐标原点, , 直线与轴分别交于两点,则以下选项正确的是( )A、 B、若 , 则 C、若 , 则面积的最小值为 D、四点共圆三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知向量 , , 且与共线,则 .14. 筒车亦称为“水转筒车”,一种以流水为动力,取水灌田的工具,筒车发明于隋而盛于唐,距今已有多年的历史如图,假设在水流量稳定的情况下,一个半径为米的筒车按逆时针方向做每分钟转一圈的匀速圆周运动,筒车的轴心距离水面的高度为米,设筒车上的某个盛水筒的初始位置为点水面与筒车右侧的交点 , 从此处开始计时,分钟时,该盛水筒距水面距离为 , 则 .
 15. 已知圆: , 若为直线:上的点,过点可作两条直线与圆分别切于点 , , 且为等边三角形,则实数的取值范围是 .16. 如图,某校学生在开展数学建模活动时,用一块边长为的正方形铝板制作一个无底面的正棱锥侧面为等腰三角形,底面为正边形道具,他们以正方形的几何中心为圆心,为半径画圆,仿照我国古代数学家刘徽的割圆术裁剪出份,再从中取份,并以为正棱锥的顶点,且落在底面的射影为正边形的几何中心 , 侧面等腰三角形的顶角为 , 当时,设正棱锥的体积为 , 则的最大值为 .
15. 已知圆: , 若为直线:上的点,过点可作两条直线与圆分别切于点 , , 且为等边三角形,则实数的取值范围是 .16. 如图,某校学生在开展数学建模活动时,用一块边长为的正方形铝板制作一个无底面的正棱锥侧面为等腰三角形,底面为正边形道具,他们以正方形的几何中心为圆心,为半径画圆,仿照我国古代数学家刘徽的割圆术裁剪出份,再从中取份,并以为正棱锥的顶点,且落在底面的射影为正边形的几何中心 , 侧面等腰三角形的顶角为 , 当时,设正棱锥的体积为 , 则的最大值为 .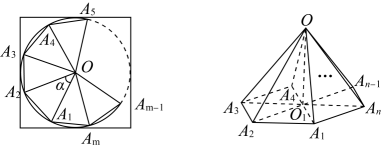
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 在中, , , 分别是的内角 , , 所对的边,且(1)、求角的大小(2)、记的面积为 , 若 , 求的最小值.18. 已知数列满足(1)、判断数列是否是等比数列?若是,给出证明;否则,请说明理由;(2)、若数列的前10项和为361,记 , 数列的前项和为 , 求证:.19. 如图,该几何体是由等高的半个圆柱和个圆柱拼接而成,点为弧的中点,且 , , , 四点共面.
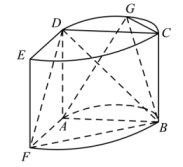 (1)、证明:平面平面;(2)、若平面与平面所成二面角的余弦值为 , 且线段长度为 , 求点到直线的距离.20. 第届世界杯于年月日到月日在卡塔尔举办.在决赛中,阿根廷队通过点球战胜法国队获得冠军.
(1)、证明:平面平面;(2)、若平面与平面所成二面角的余弦值为 , 且线段长度为 , 求点到直线的距离.20. 第届世界杯于年月日到月日在卡塔尔举办.在决赛中,阿根廷队通过点球战胜法国队获得冠军. (1)、扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数的分布列和期望;(2)、好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外人中的人,接球者接到球后再等可能地随传向另外人中的人,如此不停地传下去,假设传出的球都能接住.记第次传球之前球在甲脚下的概率为 , 易知 .
(1)、扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数的分布列和期望;(2)、好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外人中的人,接球者接到球后再等可能地随传向另外人中的人,如此不停地传下去,假设传出的球都能接住.记第次传球之前球在甲脚下的概率为 , 易知 .试证明:为等比数列;
设第次传球之前球在乙脚下的概率为 , 比较与的大小.