上海市金山区2024届高三上学期一模数学试题
试卷更新日期:2024-01-20 类型:高考模拟
一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸的相应位置直接填写结果.
-
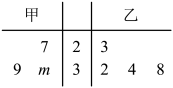
1. 已知集合A={1,2,3},B={3,4,5},则A∩B= .2. 在复平面内,复数对应的点的坐标是 , 则的共轭复数=.3. 不等式的解集为 .4. 双曲线的离心率为 .5. 已知角 , 的终边关于原点O对称,则 .6. 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,则图中的值 .
 7. 设圆台的上底面和下底面的半径分别为和 , 母线长为 , 则该该圆台的高为.8. 从1,2,3,4,5这五个数中随机抽取两个不同的数,则所抽到的两个数的和大于6的概率为(结果用数值表示).9. 已知函数()在区间上是严格增函数,且其图像关于点对称,则的值为 .10. 若 , 则.11. 若函数 的图像关于直线对称,且该函数有且仅有7个零点,则的值为 .12. 已知平面向量、、满足 , 且 , 则的取值范围是 .
7. 设圆台的上底面和下底面的半径分别为和 , 母线长为 , 则该该圆台的高为.8. 从1,2,3,4,5这五个数中随机抽取两个不同的数,则所抽到的两个数的和大于6的概率为(结果用数值表示).9. 已知函数()在区间上是严格增函数,且其图像关于点对称,则的值为 .10. 若 , 则.11. 若函数 的图像关于直线对称,且该函数有且仅有7个零点,则的值为 .12. 已知平面向量、、满足 , 且 , 则的取值范围是 .二、选择题(本题共有4题,满分18分,13、14每题4分,15、16题每题5分)每题有且只有一个正确选项,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.
-
13. 对于实数 ,“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 已知事件A和B相互独立,且 , 则( )A、 B、 C、 D、15. 如图,在正方体中,E、F为正方体内(含边界)不重合的两个动点,下列结论错误的是( ).
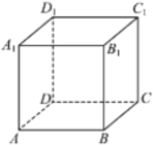 A、若 , , 则 B、若 , , 则平面平面 C、若 , , 则面 D、若 , , 则16. 设集合 , 、均为的非空子集(允许).中的最大元素与中的最小元素分别记为 , 则满足的有序集合对的个数为( ).A、 B、 C、 D、
A、若 , , 则 B、若 , , 则平面平面 C、若 , , 则面 D、若 , , 则16. 设集合 , 、均为的非空子集(允许).中的最大元素与中的最小元素分别记为 , 则满足的有序集合对的个数为( ).A、 B、 C、 D、三、解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
-
17. 如图,在四棱锥中,底面为正方形,平面 , 为的中点,为与的交点.
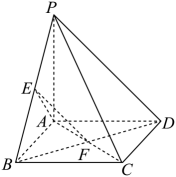 (1)、证明://平面;(2)、求三棱锥的体积.18. 已知数列满足 , 且 .(1)、求的值;(2)、若数列为严格增数列,其中是常数,求的取值范围.19. 网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图.
(1)、证明://平面;(2)、求三棱锥的体积.18. 已知数列满足 , 且 .(1)、求的值;(2)、若数列为严格增数列,其中是常数,求的取值范围.19. 网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图. (1)、为避免冰箱内部制冷液逆流,要求运送过程中发生倾斜时,外包装的底面与地面的倾斜角不能超过 , 且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形 , , , 而客户家门高度为米,其他过道高度足够.若以倾斜角的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.(2)、由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为米.记此冰箱水平截面为矩形 , . 设 , 当冰箱被卡住时(即点、分别在射线、上,点在线段上),尝试用表示冰箱高度的长,并求出的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到)20. 已知三条直线()分别与抛物线交于点、 , 为轴上一定点,且 , 记点到直线的距离为 , △的面积为 .(1)、若直线的倾斜角为 , 且过抛物线的焦点 , 求直线的方程;(2)、若 , 且 , 证明:直线过定点;(3)、当时,是否存在点 , 使得 , , 成等比数列, , , 也成等比数列?若存在,请求出点的坐标;若不存在,请说明理由.21. 设函数的定义域为 , 给定区间 , 若存在 , 使得 , 则称函数为区间上的“均值函数”,为函数的“均值点” .(1)、试判断函数是否为区间上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;(2)、已知函数是区间上的“均值函数”,求实数的取值范围;(3)、若函数(常数)是区间上的“均值函数”,且为其“均值点” . 将区间任意划分成()份,设分点的横坐标从小到大依次为 , 记 , , . 再将区间等分成()份,设等分点的横坐标从小到大依次为 , 记 . 求使得的最小整数的值 .
(1)、为避免冰箱内部制冷液逆流,要求运送过程中发生倾斜时,外包装的底面与地面的倾斜角不能超过 , 且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形 , , , 而客户家门高度为米,其他过道高度足够.若以倾斜角的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.(2)、由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为米.记此冰箱水平截面为矩形 , . 设 , 当冰箱被卡住时(即点、分别在射线、上,点在线段上),尝试用表示冰箱高度的长,并求出的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到)20. 已知三条直线()分别与抛物线交于点、 , 为轴上一定点,且 , 记点到直线的距离为 , △的面积为 .(1)、若直线的倾斜角为 , 且过抛物线的焦点 , 求直线的方程;(2)、若 , 且 , 证明:直线过定点;(3)、当时,是否存在点 , 使得 , , 成等比数列, , , 也成等比数列?若存在,请求出点的坐标;若不存在,请说明理由.21. 设函数的定义域为 , 给定区间 , 若存在 , 使得 , 则称函数为区间上的“均值函数”,为函数的“均值点” .(1)、试判断函数是否为区间上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;(2)、已知函数是区间上的“均值函数”,求实数的取值范围;(3)、若函数(常数)是区间上的“均值函数”,且为其“均值点” . 将区间任意划分成()份,设分点的横坐标从小到大依次为 , 记 , , . 再将区间等分成()份,设等分点的横坐标从小到大依次为 , 记 . 求使得的最小整数的值 .