内蒙古锡林郭勒盟2024届高三上学期第二次统一考试(全国乙卷)文科数学试题
试卷更新日期:2024-01-20 类型:高考模拟
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 若(是虚数单位),则( )A、 B、 C、 D、2. 若全集 , 则( )A、 B、 C、 D、3. 已知 , 则( )A、1 B、-2 C、-1 D、4. 造纸术是我国古代四大发明之一,纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以 , 等标记来表示纸张的幅面规格,其中系列的幅面规格为:①规格的纸张的幅宽(以表示)和长度(以表示)的比例关系为;②将纸张沿长度方向对开成两等份,便成为规格,纸张沿长度方向对开成两等份,便成为规格,的如此对开至规格.若纸的面积为 , 则纸的面积为( )A、 B、 C、 D、5. 如图,在Rt中,是直角,的内切圆与分别切于点 , 点是图中阴影区域内的一点(不包含边界).若 , 则至少满足( )
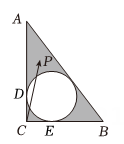 A、 B、 C、 D、6. 已知指物线第一象限上一点到其焦点的距离为10,则点的纵坐标为( )A、 B、4 C、 D、8
A、 B、 C、 D、6. 已知指物线第一象限上一点到其焦点的距离为10,则点的纵坐标为( )A、 B、4 C、 D、8
7. 已知函数 , 在以下四个选项中,错误的选项是( )A、 B、若关于的方程有两解,则 C、在上是减函数 D、若 , 则8. 已知一个正四棱锥的底面边长为2,侧面与底面所成角的大小为 , 则该四棱锥的侧棱与底面所成角的正切值为( )A、 B、 C、3 D、6
9. 设是两条异面直线,下列命题中正确的是( )A、过且与平行的平面有且只有一个 B、过且与垂直的平面有且只有一个 C、过空间一点与均相交的直线有且只有一条 D、过空间一点与均平行的平面有且只有一个10. 2013年华人数学家张益唐证明了孪生素数(素数即质数)猜想的一个弱化形式.素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷个素数 , 使得是素数,素数对称为孪生素数.则从不超过18的素数中任取两个素数,这两个素数组成孪生素数对的概率为( )A、 B、 C、 D、11. 已知函数 , 若不等式对恒成立,则实数的取值范围是( )A、 B、 C、 D、12. 如图所示,“嫦娥五号”月球探测器飞行到月球附近时,首先在以月球球心为圆心的圆形轨道I上绕月球飞行,然后在点处变轨进入以为一个焦点的椭圆轨道II绕月球飞行,最后在点处变轨进入以为圆心的圆形轨道III绕月球飞行,设圆形轨道I的半径为 , 圆形轨道III的半径为 , 则下列结论中正确的序号为( )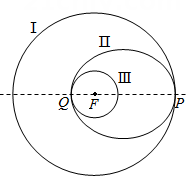
①轨道II的焦距为;
②若不变,越大,轨道II的短轴长越小;
③轨道II的长轴长为;
④若不变,越大,轨道II的离心率越大.
A、①②③ B、①②④ C、①③④ D、②③④二、选择题:本题共4小题,每小题5分,共20分.
-
13. 的三内角所对边的长分别是 , 设向量 , 若向量与向量共线,则角.14. 已知一组数据为 , 若在这组数据中插入一个自然数使得这组新数据满足中位数是7且平均数大于7,则满足上述条件的最小自然数是.15. 已知直线与函数的图象相邻的三个交点依次为 , 则.16. 设函数 , 在定义域上单调递减,则的取值范围是.
三、解答题:解答应写出文字说明,证明过程或演算步骤,第17-21题为必考题,每个考生都必须作答,第22、23题为选考题,考生根据要求作答.
-
17. 设公差不为0的等差数列中, , 且.(1)、求数列的通项公式;(2)、若数列的前项和满足: , 求数列的前项和.18. 如图所示,在四棱锥中,底面为正方形,为侧棱的中点.
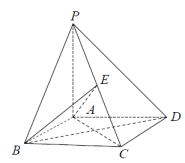 (1)、设经过三点的平面交于 , 证明:为的中点,(2)、若底面 , 且 , 求四面体的体积.19. 2023年,在第十四届全国人民代表大会常务委员会第六次会议上教育部关于考试招生制度改革情况的报告中提出:改革考试内容和形式,实现从“考知识”向“考能力素养”转变;探索拔尖创新人才超常规选鉴通道,设立清华大学数学科学领军人才培养计划、北京大学物理卓越人才培养计划等专项计划,推进拔尖创新人才选拔培养.为此,各地区高中积极推进“强基计划”的落实,“强基培训”成为学生们热爱的课程之一.某高中随机调研了本校2023年参加高考的90位考生是否参加“强基培训”的情况,经统计,“强基培训”与性别情况如下表:(单位:人)
(1)、设经过三点的平面交于 , 证明:为的中点,(2)、若底面 , 且 , 求四面体的体积.19. 2023年,在第十四届全国人民代表大会常务委员会第六次会议上教育部关于考试招生制度改革情况的报告中提出:改革考试内容和形式,实现从“考知识”向“考能力素养”转变;探索拔尖创新人才超常规选鉴通道,设立清华大学数学科学领军人才培养计划、北京大学物理卓越人才培养计划等专项计划,推进拔尖创新人才选拔培养.为此,各地区高中积极推进“强基计划”的落实,“强基培训”成为学生们热爱的课程之一.某高中随机调研了本校2023年参加高考的90位考生是否参加“强基培训”的情况,经统计,“强基培训”与性别情况如下表:(单位:人)参加“强基培训”
不参加“强基培训”
男生
25
35
女生
5
25
(1)、根据表中数据并依据小概率值的独立性检验,分析参加“强基培训”与性别是否有关联?(2)、在本校被调研的90位考生中,先对多加“强基培训”的30人采用分层抽样的方法抽取6位同学,然后从这6名同学中选拔2人参加北京大学物理卓越人才培养计划专项计划的招生考试,求有女生参加北京大学物理卓越人才培养计划专项计划的招生考试的概率.0.10
0.05
0.025
0.010
0.005
2.706
3.841
5.024
6.635
7.879
20. 设椭圆的左焦点为 , 左顶点为 , 上顶点为 , 已知(为原点).(1)、求椭圆的离心率;(2)、设经过点且斜率为的直线与椭圆在轴上方的交点为 , 圆同时与轴和直线相切,圆心在直线上,且 , 求椭圆的方程.