广西壮族自治区柳州市鹿寨县2023-2024学年九年级上学期1月期末数学试题

试卷更新日期：2024-01-20 类型：期末考试

进入出卷网下载

一、单选题（共12小题，每小题3分，共36分

1. 下列图形是我国国产品牌汽车的标识，这些汽车标识中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程属于一元二次方程的是（）

A、 $x y = 9$ B、 $x + y = 9$ C、 $x^{2} + 2 x = 0$ D、 $x + \frac{1}{x} = 9$

查看试题解析
3. 一个扇形的半径是 $3$ ，扇形的圆心角 $120 °$ ，那么这个扇形面积是（）

A、 $4 π$ B、 $3 π$ C、 $2 π$ D、 $π$

查看试题解析
4. 已知一元二次方程 $x^{2} - 4 x + 2 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为（）

A、 $6$ B、 $- 6$ C、 $2$ D、 $- 2$

查看试题解析
5. 如图，A ， B ， C是 $⊙ O$ 上的三个点．若 $∠ B = 30 °$ ，则 $∠ A O C$ 的度数为（　　）

A、 $60 °$ B、 $50 °$ C、 $30 °$ D、 $15 °$

查看试题解析
6. 下列语句描述的事件中，是随机事件的为（）

A、少年强则国强 B、水中捞月 C、守株待兔 D、绿水青山就是金山银山

查看试题解析
7. 反比例函数 $y = \frac{4}{x}$ 的图象经过下列哪个点？（　　）

A、 $(1 ， 2)$ B、 $(2 ， 2)$ C、 $(- 2 ， 2)$ D、 $(2 ， - 2)$

查看试题解析
8. 如图， $A B$ 为 $⊙ O$ 的弦，直径 $C D ⊥ A B$ ，交 $A B$ 于点 $H$ ，连接 $O A$ ，若 $∠ A = 45 °$ ， $A B = 2$ ， $D H$ 的长度为（）

A、1 B、 $\sqrt{2} - 1$ C、 $\sqrt{2} + 1$ D、3

查看试题解析
9. 已知 $x = - 1$ 是一元二次方程 $x^{2} + m x = 3$ 的一个解，则 $m$ 的值是（）

A、 $0$ 或 $2$ B、 $2$ C、 $0$ D、 $- 2$

查看试题解析
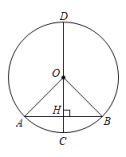10. 电影《志愿军：雄兵出击》于2023年9月28日上映，首周票房约 $2.5$ 亿，第三周票房约 $3.6$ 亿，若每周票房按相同的增长率增长，设增长率为 $x$ ，则根据题意可列方程为（）

A、 $2.5 (1 + x) = 3.6$ B、 $2.5 {(1 + x)}^{2} = 3.6$ C、 $2.5 + 2.5 (1 + x) = 3.6$ D、 $2.5 + 2.5 (1 + x) + 2.5 {(1 + x)}^{2} = 3.6$

查看试题解析
11. 铅球运动员掷铅球的高度 $y$ （m）与水平距离 $x$ （m）之间的函数关系式为 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该运动员此次掷铅球的成绩是（）

A、 $\frac{10}{3} m$ B、8m C、10m D、12m

查看试题解析
12. 若二次函数 $y = a x^{2} + b x + c$ 的图象如图，与x轴的一个交点为（1，0），则下列各式中不成立的是（）

A、 $b^{2} - 4 a c > 0$ B、 $a b c > 0$ C、 $a + b + c = 0$ D、 $a - b + c < 0$

查看试题解析

二、填空题（共6小题，每小题2分，共12分）

13. 在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是

查看试题解析
14. 若⊙O的半径为3，点P为平面内一点，OP＝2，那么点P在⊙O（填“上”、“内部”或“外部”）

查看试题解析
15. 抛物线 $y = - 3 {(x - 1)}^{2} + 4$ 的顶点坐标是．

查看试题解析
16. 关于x的方程 $m x^{2} - 2 x + 5 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
17. 如图， $△ A B C ≌ △ A D E$ ， $∠ B = 30 °$ ， $∠ C = 95 °$ ，则 $∠ E A D$ 的度数为．

查看试题解析
18. 如图，点A ， C分别是y轴，x轴正半轴上的动点， $A C = 1$ ，将线段 $A C$ 绕点A顺时针旋转60°得到线段 $A B$ ，则 $O B$ 的最小值是．

查看试题解析

三、解答题（本大题共7小题，共72分）

19. 解方程： $x^{2} - 2x - 1 = 0$

查看试题解析
20. 如图是一个矩形花圃，它的两边分别长为10 m和6 m，现要在花圃内铺设一条互相垂直的十字石子路，横竖路面宽度相等．若要使种花的面积是45 m² ，石子路的宽度应是多少？

查看试题解析
21. 为大力弘扬“奉献、友爱、互助、进步”的志愿精神，我市某社区开展了“文明新风进社区”系列志愿服务活动，参加活动的每位志愿者必须从A ． “垃圾分类入户宣传”、B ． “消防安全知识宣传”、C ． “走访慰问孤寡老人”、D ． “社区环境整治活动”四个活动主题中随机选取一个主题中随机选取一个主题．

(1)、志愿者小李选取A ． “垃圾分类入户宣传”这个主题的概率是．

(2)、志愿者小张和小李从A、B、C、D四个主题中分别随机选取一个主题，请用列表或画树状图的方法，求他们选取相同主题的概率．

查看试题解析
22. 如图，一次函数 $y = k x + b$ 的图象交y轴于点 $C (0 ， 2)$ ，与反比例函数 $y = \frac{m}{x}$ 的图象交于A ， B两点，且A点坐标为 $(- 3 ， - 1)$ ．

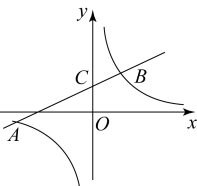(1)、确定上述反比例函数和一次函数的表达式；

(2)、直接写出不等式 $k x + b < \frac{m}{x}$ 的解集．

查看试题解析
23.
如图，在 $10 \times 10$ 的正方形网格中（每个小正方形的边长都为1），点 $O$ ， $B$ ， $C$ 均在格点上．

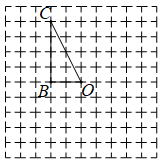(1)、在网格图中画出 $△ O B C$ 绕点 $O$ 顺时针旋转90°后的 $△ O B_{1} C_{1}$ ．

(2)、在（1）的条件下，求旋转过程中，点 $C$ 所经过的弧长．（结果保留 $π$ ）

查看试题解析
24.
如图，四边形 $A B C D$ 的两条对角线 $A C$ ， $B D$ 互相垂直，垂足为 $O$ 点，且 $A C + B D = 10$ ，若四边形 $A B C D$ 有最大面积，则求出此时的 $A C$ 与 $B D$ 的长及这个最大的面积．

查看试题解析
25.
如图， $A B$ 是 $⊙ O$ 的直径， $F$ 为⨀O上一点， $A C$ 平分 $∠ F A B$ 交⨀O于点 $C$ ，过点 $C$ 作 $C D ⊥ A F$ 交 $A F$ 的延长线于点 $D$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线．

(2)、若 $D C = 3$ ， $A D = 9$ ，求 $⊙ O$ 半径．

查看试题解析
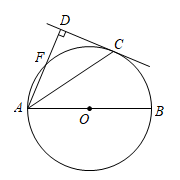26. 动手操作：某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘．
如图1，△ACB是等腰直角三角形，AC＝BC＝4，∠ACB＝90°，将边AB绕点B顺时针旋转90°得到线段A′B ，连接A′C ，过点A′作A′D⊥CB交CB延长线于点D ．

(1)、在图1中：△A′BC的面积为；

(2)、如图2，若△ACB为任意直角三角形，∠ACB＝90°．将边AB绕点B顺时针旋转90°得到线段A′B ，连接A′C ，过点A′作A′D⊥CB交CB延长线于点D ．猜想三条线段AC、CD、A′D的数量关系，并证明．

(3)、如图3，在△ACB中，AB＝AC＝5，BC＝6，将边AB绕点B顺时针旋转90°得到线段A′B ，连接A′C ．
若点D是△ACB的边BC的高线上的一动点，连接A′D、DB ，则A′D+DB的最小值是．

查看试题解析