2023-2024学年人教版初中数学九年级下册27.2.3 相似三角形应用举例 同步分层训练培优题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，则树的高度为（ ）
A、4.8m B、6.4m C、8m D、10m2.如图，小明在打网球时，使球恰好能打过网，而且落点恰好在离网6米的位置上，则球拍击球的高度h为( )
A、米 B、1米 C、米 D、米3.电影胶片上每一个图片的规格为3.5cm×3.5cm，放映屏幕的规格为2m×2m，若放映机的光源S距胶片20cm，要使放映的图象刚好布满整个屏幕，则光源S距屏幕的距离为（ ）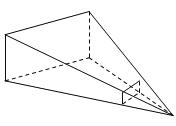
A、m B、m C、m D、15m4. “差之毫厘，失之千里”是一句描述开始时虽然相差很微小，结果会造成很大的误差或错误的成语.现实中就有这样的实例，如步枪在瞄准时的示意图如图，从眼睛到准星的距离OE为80cm，眼睛距离目标为200m，步枪上准星宽度AB为2mm，若射击时，由于抖动导致视线偏离了准星1mm，则目标偏离的距离为（ ）cm．A、25 B、50 C、75 D、1005.如图，矩形AEHC是由三个全等矩形拼成的AH与BE ， BF ， DF ， DG ， CG分别交于点P ， Q ， K ， M ， N ， 设△BPQ ， △DKM ， △CNH 的面积依次为S1 ， S2 ， S3. 若S1+ S3=20，则S2的值为( )
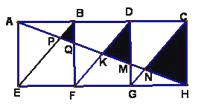A、8 B、12 C、10 D、6.如图，在平面直角坐标系xOy中，A(2，0)，B(0，2)，⊙C的圆心为点C(-1，0)，半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E ， 则△ABE面积的最小值是（ ）
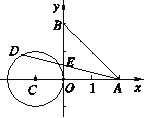A、2 B、 C、 D、7. 一块直角三角形木板，它的一条直角边AC长为1cm，面积为1cm2 ， 工人分别按图中甲、乙两种方式把它加工成一个正方形桌面，则正方形的面积较大的是（ ）.
A、甲 B、乙 C、一样大 D、无法判断8. 如图，正方形ABCD中，E为BC的中点，CG⊥DE于G，BG延长交CD于点F，CG延长交BD于点H，交AB于N.下列结论：①DE=CN；② ；③S△DEC=3S△BNH；④∠BGN=45°；⑤ .其中正确结论的个数有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理．小孔成像的示意图如图所示，光线经过小孔O ， 物体AB在幕布上形成倒立的实像CD（点A、B的对应点分别是C、D）．若物体AB的高为6cm ， 小孔O到物体和实像的水平距离BE、CE分别为8cm、6cm ， 则实像CD的高度为 cm ．
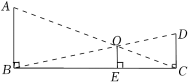
10. 如图，小明在测得某树的影长为 ， 时又测得该树的影长为 ， 若两次日照的光线互相垂直，则这棵树的高度为 ．
11. 如图是用杠杆撬石头的示意图，当用力压杠杆时，杠杆绕着支点转动，另一端会向上翘起，石头就被翘动了在图中，杠杆的端被向上翘起的距离 ， 动力臂与阻力臂满足与相交于点 ， 要把这块石头翘起，至少要将杠杆的点向下压 ．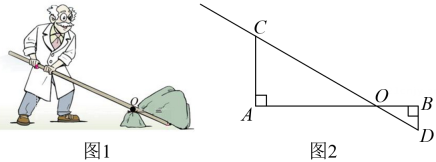
12. 如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥I，BF⊥I，点N，A，B在同一直线上。在F点观测A点后，沿FN方向走到M点，观测C点发现∠1=∠2测得EF=15米，FM=2米，MN=8米，∠ANE=45°。
(1)、AB为米；(2)、矩形ABCD的面积为米2。13.如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为 ．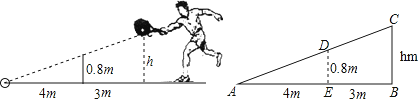
三、解答题
-
14. 小玲和晓静很想知道某塔的高度PQ，于是，他们带着标杆和皮尺进行测量，测量方案如下：如图所示，首先，小玲在处放置一平面镜，她从点沿QC后退，当退行到处时，恰好在镜子中看到塔顶的像，此时测得小玲眼睛到地面的距离AB为；然后，晓静在处竖立了一根高的标杆EF，发现地面上的点、标杆顶点和塔顶在一条直线上，此时测得FM为为 ， 已知 ， 点Q，C，B，F，M在一条直线上，请根据以上所测数据，计算该塔的高度PQ.
15. 在中， ， 是边的中点，以为角的顶点作.如图1，射线经过点 ， 交边于点.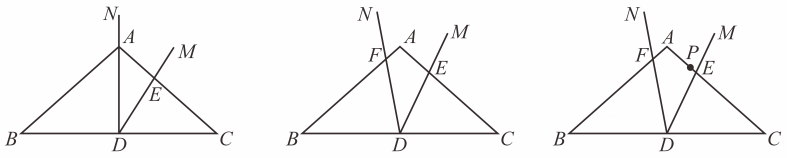
图1 图2 图3
(1)、不添加辅助线，请直接写出图1中所有与相似的三角形；(2)、如图2，将从图1中的位置开始，绕点按逆时针方向旋转（旋转角不大于），射线 ， 分别交 ， 于点 ， .①求证：；
②如图3，若 ， ， 在线段上有一点 ， 且 ， 若点始终在内（包括边界上），求的取值范围；
③若 ， 直接写出旋转角为多少度时，与相似.
四、综合题
-
16. 如图1，点光源O射出光线沿直线传播，将胶片上的建筑物图片AB投影到与胶片平行的屏幕上，形成影像CD. 已知AB＝0.3 dm，胶片与屏幕的距离EF为定值，设点光源到胶片的距离OE长为x（单位：dm），CD长为y（单位：dm），当x＝6时，y＝4.3.
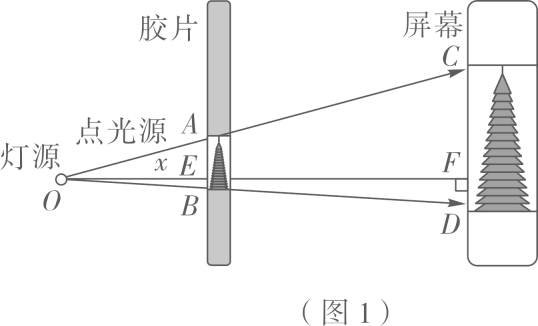
(1)、求EF的长.(2)、求y关于x的函数解析式，在图2中画出图象，并写出至少一条该函数性质．(3)、若要求CD不小于3 dm，求OE的取值范围.17. 如图，AB是⊙O的直径，点E在AB的延长线上，AC平分∠DAE交⊙O于点C，AD⊥DE于点D．
（l）求证：直线DE是⊙O的切线．
(1)、如果BE=2，CE=4，求线段AD的长．