人教版数学九年级下册27.2.3 相似三角形应用举例 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 如图所示,某校数学兴趣小组利用标杆BE测量物的高度,已知标杆BE高1.5m,测得AB=1.2m,AC=14m,则建筑物CD的高是( )
 A、17.5m B、17m C、16.5m D、18m2. 高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )A、10米 B、16米 C、26米 D、36米3. 如图,为估算学校的旗杆的高度,身高 米的小红同学沿着旗杆在地面的影子 由 向 走去,当她走到点 处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得 , ,则旗杆的高度是( )
A、17.5m B、17m C、16.5m D、18m2. 高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )A、10米 B、16米 C、26米 D、36米3. 如图,为估算学校的旗杆的高度,身高 米的小红同学沿着旗杆在地面的影子 由 向 走去,当她走到点 处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得 , ,则旗杆的高度是( ) A、6.4m B、7m C、8m D、9m4. 如图,为测量学校旗杆的高度,小明用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
A、6.4m B、7m C、8m D、9m4. 如图,为测量学校旗杆的高度,小明用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )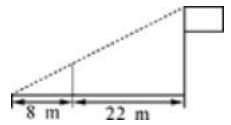 A、8.8m B、10m C、12m D、14m5. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( )
A、8.8m B、10m C、12m D、14m5. 如图,一壁厚均匀的容器外径为18 , 用一个交叉卡钳(两条尺长和相等)可测量容器的内部直径.如果 , 且量得 , 则零件的厚度x为( ) A、0.25 B、0.3 C、0.35 D、0.46. 同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为 ( )A、0.8米 B、6.4米 C、12.8米 D、25.6米7. 如图1,是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面的宽度为( )
A、0.25 B、0.3 C、0.35 D、0.46. 同一时刻,同一地点,在阳光下影长为0.4米的小王身高为1.6米,一棵树的影长为3.2米,则这棵树的高度为 ( )A、0.8米 B、6.4米 C、12.8米 D、25.6米7. 如图1,是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面的宽度为( )
图1 图2
A、 B、 C、 D、8. 如图,一张等腰三角形纸片,底边长为15cm,底边上的高线长为22.5cm.现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ). A、第4张 B、第5张 C、第6张 D、第7张
A、第4张 B、第5张 C、第6张 D、第7张二、填空题
-
9. 如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退保持脚、镜和旗杆底端在同一直线上 , 直到她刚好在镜子中看到旗杆的顶端已知小艺的眼睛离地面高度为米,同时量得小艺与镜子的水平距离为米,镜子与旗杆的水平距离为米,则旗杆的高度为 米
 10. 如图,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退,直到她刚好在镜子中看到旗杆的顶端,已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米.则旗杆的高度为 米.
10. 如图,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退,直到她刚好在镜子中看到旗杆的顶端,已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米.则旗杆的高度为 米. 11. 如下图,跷跷板支架的高为0.3米,是的中点,那么跷跷板能骁起的最大高度等于米.
11. 如下图,跷跷板支架的高为0.3米,是的中点,那么跷跷板能骁起的最大高度等于米. 12. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.
12. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.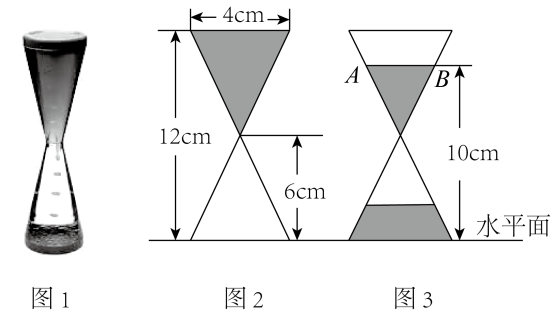 13. 如图,某公园有一月牙形水池,水池边缘有A , B , C , D , E五盏装饰灯.为了估测该水池的大小,观测员在A , D两点处发现点A , E , C和D , E , B均在同一直线上,沿AD方向走到F点,发现 . 测得米,米,米,则所在圆的半径为米,所在圆的半径为.米.
13. 如图,某公园有一月牙形水池,水池边缘有A , B , C , D , E五盏装饰灯.为了估测该水池的大小,观测员在A , D两点处发现点A , E , C和D , E , B均在同一直线上,沿AD方向走到F点,发现 . 测得米,米,米,则所在圆的半径为米,所在圆的半径为.米.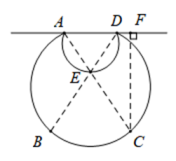
三、解答题
-
14. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长.
 15. 一天晚上,小南和小北利用灯光下的影子来测量一路灯D的高度,如图,当朝阳走到点A处时,小南测得小北直立身高AM与其影子长AE正好相等,接着小北沿AC方向继续向前走,走到点B处时,小北直立时身高BN的影子恰好是线段AB,并测得.已知小北直立时的身高为1.5m,求路灯的高CD的长.
15. 一天晚上,小南和小北利用灯光下的影子来测量一路灯D的高度,如图,当朝阳走到点A处时,小南测得小北直立身高AM与其影子长AE正好相等,接着小北沿AC方向继续向前走,走到点B处时,小北直立时身高BN的影子恰好是线段AB,并测得.已知小北直立时的身高为1.5m,求路灯的高CD的长.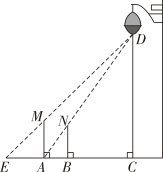
四、综合题


